Algorithms in the Splunk Machine Learning Toolkit
The Splunk Machine Learning Toolkit (MLTK) supports all of the algorithms listed here. Details for each algorithm are grouped by algorithm type including Anomaly Detection, Classifiers, Clustering Algorithms, Cross-validation, Feature Extraction, Preprocessing, Regressors, Time Series Analysis, and Utility Algorithms. You can find more examples for these algorithms on the scikit-learn website.
MLTK supported algorithms use the fit and apply commands. For information on the steps taken by these commands, see About the fit and apply commands.
For information on using the score command, see Scoring metrics in the Splunk Machine Learning Toolkit.
ML-SPL Quick Reference Guide
Download the Splunk Machine Learning Toolkit Quick Reference Guide for a handy cheat sheet of current ML-SPL commands and machine learning algorithms available in the Splunk Machine Learning Toolkit. This document is also offered in Japanese.
Extend the algorithms you can use for your models
The algorithms listed here and in the ML-SPL Quick Reference Guide are available natively in the Splunk Machine Learning Toolkit. You can also base your algorithm on over 300 open source Python algorithms from scikit-learn, pandas, statsmodel, numpy and scipy libraries available through the Python for Scientific Computing add-on in Splunkbase.
For information on how to import an algorithm from the Python for Scientific Computing add-on into the Splunk Machine Learning Toolkit, see the ML-SPL API Guide.
Add algorithms through GitHub
On-premises customers looking for solutions that fall outside of the algorithms that ship with MLTK can use GitHub to add more algorithms. Join the Splunk Community for MLTK on GitHub. to also learn about new machine learning algorithms, solve custom uses cases through sharing and reusing algorithms, and help fellow users of MLTK.
Splunk Cloud Platform customers can also use GitHub to add more algorithms using an app. The Splunk GitHub for Machine learning app provides access to custom algorithms and is based on the Machine Learning Toolkit open source repo. Splunk Cloud Platform customers must create a support ticket to have this app installed.
Anomaly Detection
Anomaly detection algorithms detect anomalies and outliers in numerical or categorical fields.
DensityFunction
The DensityFunction algorithm provides a consistent and streamlined workflow to create and store density functions and utilize them for anomaly detection. DensityFunction allows for grouping of the data using the by clause, where for each group a separate density function is fitted and stored. This algorithm supports incremental fit.
The DensityFunction algorithm supports the following continuous probability density functions: Normal, Exponential, Gaussian Kernel Density Estimation (Gaussian KDE), and Beta distribution.
Using the DensityFunction algorithm requires running version 1.4 or higher of the Python for Scientific Computing add-on.
The accuracy of the anomaly detection for DensityFunction depends on the quality and the size of the training dataset, how accurately the fitted distribution models the underlying process that generates the data, and the value chosen for the threshold parameter.
Follow these guidelines to make your models perform more accurately:
- Aim for fitted distributions to have a cardinality (training dataset size) of at least 50. If you cannot collect more training data, create fewer groups of data using the
byclause, giving you more data points per group. - The
thresholdparameter has a default value, but ideally the value forthreshold,lower_threshold, orupper_thresholdare chosen based on experimentation as guided by domain knowledge. - Continue tuning the
thresholdparameter until you are satisfied with the results. - Inspect the model using the
summarycommand.- The values reported for the mean and standard deviation are either the statistics of the fitted distribution, or of the data, depending on the type of the distribution.
- In the case of parametric distributions (Normal, Beta, and Exponential) the mean and standard deviation are calculated from the fitted distribution. When the parametric distribution is not a good fit for the data, the reported mean and std might not be close to that of data.
- In the case of non-parametric distributions (Gaussian KDE) the mean and standard deviation are calculated from the data passed in during
fit.
- If the distribution of the data changes through time, re-train your models frequently.
Parameters
- The
partial_fitparameter controls whether an existing model should be incrementally updated on not. This allows you to update an existing model using only new data without having to retrain it on the full training data set.- The
partial_fitparameter default is False. - If
partial_fitis not specified, the model specified is created and replaces the pre-trained model if one exists.
- The
- Using
partial_fit=Trueon an existing model ignores the newly supplied parameters. The parameters supplied at model creation are used instead. - The
supervise_split_byparameter is available with MLTK version 5.5.0 or higher and this parameter can be set to true or false.- When set to true, the fields entered in the
byclause are used by a decision tree algorithm to automatically generate groups in the dataset
- When set to true, the fields entered in the
- Valid values for the
distparameter include:norm(normal distribution),expon(exponential distribution),gaussian_kde(Gaussian KDE distribution),beta(beta distribution), andauto(automatic selection).- The
distparameter default isauto. - When set to
auto,norm(normal distribution),expon(exponential distribution),gaussian_kde(Gaussian KDE distribution) , andbeta(beta distribution) all run, with the best results returned.
- The
- Use the
exclude_distparameter to exclude a minimum of 1 and a maximum of 3 of the available dist parameter values (norm, expon, gaussian_kde, beta).- The
exclude_distparameter is only available when the dist parameter isauto. - DensityFunction will run using any non-excluded dist parameter values.
- Use a comma to note multiple excluded dist parameter values. For example,
exclude_dist="beta,expon" - Attempts to use the
exclude_distparameter on more than 3 dist parameter values, or on a dist parameter other thanautowill result in an error message.
- The
- Beta distribution was added in version 5.2.0 of the Machine Learning Toolkit
- If the data distribution takes a U shape, outlier detection will not be accurate.
- The
metricparameter calculates the distance between the sampled dataset from the density function and the training dataset. - Valid metrics for the
metricparameter include: kolmogorov_smirnov and wasserstein. - The
metricparameter default is wasserstein. - The
sampleparameter can be used duringfitorapplystages. - The
sampleparameter default is False. - If the
sampleparameter is set to True during thefitstage, the size of the samples will be equal to the training dataset. - If the
sampleparameter is set to True during theapplystage, the size of the samples will be equal to the testing dataset. - If the
sampleparameter is set to True:- Samples are taken from the fitted density function.
- Results output in a new column called
SampledValue. - Sampled values only come from the inlier region of the distribution.
- The
full_sampleparameter can be used duringfitorapplystages. - The
full_sampleparameter default is False. - If the
full_sampleparameter is set to True during the fit stage, the size of the samples will be equal to the training dataset. - If the
full_sampleparameter is set to True during the apply stage, the size of the samples will be equal to the testing dataset. - If the
full_sampleparameter is set to True:- Samples are taken from the fitted density function.
- Results output in a new column called
FullSampledValue. - Sampled values come from the whole distribution (both inlier and outlier regions).
- Use the
summarycommand to inspect the model.- The values reported for the mean and standard deviation are either the statistics of the fitted distribution, or of the data, depending on the type of the distribution.
- In the case of parametric distributions (Normal, Beta, and Exponential) the mean and standard deviation are calculated from the fitted distribution. When the parametric distribution is not a good fit for the data, the reported mean and std might not be close to that of data.
- In the case of non-parametric distributions (Gaussian KDE) the mean and standard deviation are calculated from the data passed in during
fit.
- Version 4.4.0 and higher of MLTK support min and max values in
summary.- The
minvalue is the minimum value of the dataset on which the density function is fitted. - The
maxvalue is the maximum value of the dataset on which the density function is fitted.
- The
- The
cardinalityvalue generated by thesummarycommand represents the number of data points used when fitting the selected density function. - The
distancevalue generated by thesummarycommand represents the metric type used when calculating the distance as well as the distance between the sampled data points from the density function and the training dataset. - The
meanvalue generated by thesummarycommand is the mean of the density function. - The value for
stdgenerated by thesummarycommand represents the standard deviation of the density function. - A value under
otherrepresents any parameters other thanmeanandstdas applicable. In the case of Gaussian KDE,othercould show parameter size or bandwidth. - The
typefield generated by thesummarycommand shows both the chosen density function as well as if thedistparameter is set to auto. - The
show_densityparameter default is False. If the parameter is set to True, the density of each data point will be provided as output in a new field calledProbabilityDensity. - The output for
ProbabilityDensityis the probability density of the data point according to the fitted probability density. This output is provided when theshow_densityparameter is set to True. - The
fitcommand will fit a probability density function over the data, optionally store the resulting distribution's parameters in a model file, and output the outlier in a new field calledIsOutlier. - The output for
IsOutlieris a list of labels. Number 1 represents outliers, and 0 represents inliers, assigned to each data point. Outliers are detected based on the values set for thethresholdparameter. Inspect theIsOutlierresults column to see how well the outlier detection is performing. - The parameters
threshold,lower_threshold, andupper_thresholdcontrol the outlier detection process. - The
thresholdparameter is the center of the outlier detection process. It represents the percentage of the area under the density function and has a value between 0.000000001 (refers to ~0%) and 1 (refers to 100%). Thethresholdparameter guides the DensityFunction algorithm to mark outlier areas on the fitted distribution. For example, ifthreshold=0.01, then 1% of the fitted density function will be set as the outlier area. - The
thresholdparameter default value is 0.01. - The
threshold,lower_threshold, andupper_thresholdparameters can take multiple values.- Multiple values must be in quotation marks and separated by commas.
- In cases of multiple values for
threshold, the default maximum is 5. Users with access permissions can change this default maximum under the Settings tab. - In cases of multiple values, you are limited to one type of threshold (
threshold,lower_threshold, orupper_threshold).
- The output for
BoundaryRangesis the boundary ranges of outliers on the density function which are set according to the values of thethresholdparameter. - Each boundary region has three values: boundary opening point, boundary closing point, and percentage of boundary region.
- The boundary region syntax follows the convention of a multi-value field where each boundary region appears in a new line:
first_boundary_region second_boundary_region n_th_boundary_region
- When multiple thresholds are provided, Boundary Ranges for each threshold appears in a different column separated with the suffix of
_th=and the threshold values:
BoundaryRanges_th=threshold_val_1 first_boundary_region_of_th1 second_boundary_region_of_th1 n_th_boundary_region_of_th1
BoundaryRanges_th=threshold_val_2 first_boundary_region_of_th2 second_boundary_region_of_th2 n_th_boundary_region_of_th2
- In cases of a single boundary region, the value for the percentage of boundary region is equal to the
thresholdparameter value. - In some distributions (for example Gaussian KDE), the sum of outlier areas might not add up to the exact value of
thresholdparameter value, but will be a close approximation. BoundaryRangesis calculated as an approximation and will be empty in the following two cases:- Where the density function has a sharp peak from low standard deviation.
- When there are a low number of data points.
- Data points that are exactly at the boundary opening or closing point are assigned as inliers. An opening or closing point is determined by the density function in use.
- Normal density function has left and right boundary regions. Data points on the left of the left boundary closing point, and data points on the right of the right boundary opening point are assigned as outliers.
- Exponential density function has one boundary region. Data points on the right of the right boundary opening point are assigned as outliers.
- Beta density function has one boundary region. Data points on the left of the left boundary closing point are assigned as outliers.
- Gaussian KDE density function can have one or more boundary regions, depending on the number of peaks and dips within the density function. Data points in these boundary regions are assigned as outliers. In cases of boundary regions to the left or right, guidelines from Normal density function apply. As the shape for Gaussian KDE density function can differ from dataset to dataset, you do not consistently observe left and right boundary regions.
- The
random_stateparameter is the seed of the pseudo random number generator to use when creating the model. This parameter is optional but the value must be an integer.
The random_state parameter is available in MLTK version 5.0.0 or higher. This parameter is not supported in version 4.5.0 of MLTK.
Syntax
| fit DensityFunction <field> [by "<field1>[,<field2>,....<field5>]"] [into <model name>] [dist=<str>] [show_density=true|false] [sample=true|false][full_sample=true|false][threshold=<float>|lower_threshold=<float>|upper_threshold=<float>] [metric=<str>] [random_state=<int>] [partial_fit=<true|false>]
You can apply the saved model to new data with the apply command, with the option to update the parameters for threshold, lower_threshold, upper_threshold, and show_density. Parameters for dist and metric cannot be applied at this stage, and any new values provided will be ignored.
apply <model name> [threshold=<float>|lower_threshold=<float>|upper_threshold=<float>] [show_density=true|false][sample=true|false][full_sample=true|false]
You can inspect the model learned by DensityFunction with the summary command. Version 4.4.0 or higher of MLTK supports min and max values in the summary command.
| summary <model name>
Syntax constraints
- Fields within the
byclause must be given in quotation marks. - The maximum number of fields within the
byclause is 5. - The total number of groups calculated with the
byclause can not exceed 1024. In an example clause ofby "DayOfWeek,HourOfDay"there are two fields: one forDayOfWeekand one forHourOfDay. As there are seven days in a week, there are seven groups forDayOfWeek. As there are twenty-four hours in a day, there are twenty-four groups forHourOfDay. Meaning the total number of groups calculated with the by clause is7*24= 168.- The limited number of groups prevents model files from growing too large. You can increase the limit by changing the value of
max_groupsin the DensityFunction settings. Larger limits mean larger model files and longer load times when runningapply. - Decrease
max_kde_parameter_sizeto allow for the increase ofmax_groups. This change keeps model sizes small while allowing for increased groups.
- The limited number of groups prevents model files from growing too large. You can increase the limit by changing the value of
- Field names used within the
byclause that match any one of the reserved summary field names, produces an error. You must rename your field(s) used within thebyclause to fix the error. Reserved summary field names include:type, min, max, mean, std, cardinality, distance, andother. - The parameters
threshold,lower_threshold, andupper_thresholdmust be within the range of 0.00000001 to 1. - If the parameters of
lower_thresholdandupper_thresholdare both provided, the summation of these parameters must be less than 1 (100%). - The
thresholdandlower_threshold/upper_thresholdparameters can not be specified together. - The
threshold,lower_threshold, andupper_thresholdparameters can take multiple values but in these cases you are limited to one type of threshold (threshold,lower_threshold, orupper_threshold). - Exponential density function only supports
thresholdandupper_threshold. - Exponential density function supports using
lower_thresholdbut results in empty Boundary regions and 0 outliers. - Normal density function supports either
thresholdorlower_threshold/upper_threshold. - Gaussian KDE density function supports either
thresholdorlower_threshold/upper_threshold. - The parameters
lower_thresholdandupper_thresholdcan be used with any density function including auto.- Exponential density function supports using
lower_thresholdbut results in empty Boundary regions and 0 outliers.
- Exponential density function supports using
- If you use the
summarycommand to inspect a model created in version 4.3.0 or lower of MLTK (prior to the support of min and max), approximate values for min and max are used.
Examples
The following example shows DensityFunction on a dataset with the fit command.
| inputlookup call_center.csv | eval _time=strptime(_time, "%Y-%m-%dT%H:%M:%S") | bin _time span=15m | eval HourOfDay=strftime(_time, "%H") | eval BucketMinuteOfHour=strftime(_time, "%M") | eval DayOfWeek=strftime(_time, "%A") | stats max(count) as Actual by HourOfDay,BucketMinuteOfHour,DayOfWeek,source,_time | fit DensityFunction Actual by "HourOfDay,BucketMinuteOfHour,DayOfWeek" into mymodel
The following example shows DensityFunction on a dataset with the apply command.
| inputlookup call_center.csv | eval _time=strptime(_time, "%Y-%m-%dT%H:%M:%S") | bin _time span=15m | eval HourOfDay=strftime(_time, "%H") | eval BucketMinuteOfHour=strftime(_time, "%M") | eval DayOfWeek=strftime(_time, "%A") | stats max(count) as Actual by HourOfDay,BucketMinuteOfHour,DayOfWeek,source,_time | apply mymodel show_density=True sample=True
The following example shows DensityFunction on a dataset with the summary command. This example includes min and max values, which are supported in version 4.4.0 and higher of MLTK.
| summary mymodel
The following example shows BoundaryRages on a test set. In this example the threshold is set to 30% (0.3). The first row has a left boundary range which starts at -Infinity and goes up to the number 44.6912. The area of the left boundary range is 15% of the total area under the density function. It has also a right boundary range which starts at a number 518.3088 and goes up to Infinity. Again, the area of the right boundary range is the same as the left boundary range with 15% of the total area under the density function. The areas of right and left boundary ranges add up to the threshold value of 30%. The third row has only one boundary range which starts at number 300.0943 and goes up to Infinity. The area of the boundary range is 30% of the area under the density function.
| inputlookup call_center.csv | eval _time=strptime(_time, "%Y-%m-%dT%H:%M:%S") | bin _time span=15m | eval HourOfDay=strftime(_time, "%H") | eval BucketMinuteOfHour=strftime(_time, "%M") | eval DayOfWeek=strftime(_time, "%A") | stats max(count) as Actual by HourOfDay, BucketMinuteOfHour, DayOfWeek, source, _time | fit DensityFunction Actual by "HourOfDay, BucketMinuteOfHour, DayOfWeek" threshold=0.3 into mymodel
LocalOutlierFactor
The LocalOutlierFactor algorithm uses the scikit-learn Local Outlier Factor (LOF) to measure the local deviation of density of a given sample with respect to its neighbors. LocalOutlierFactor performs one-shot learning and is limited to fitting on training data and returning outliers. LocalOutlierFactor is an unsupervised outlier detection method. The anomaly score depends on how isolated the object is with respect to its neighbors.
For descriptions of the n_neighbors, leaf_size and other parameters, see the sci-kit learn documentation: http://scikit-learn.org/stable/modules/generated/sklearn.neighbors.LocalOutlierFactor.html
Using the LocalOutlierFactor algorithm requires running version 1.3 or above of the Python for Scientific Computing add-on.
Parameters
- The
anomaly_scoreparameter default is True. Disable this default by adding theFalsekeyword to the command. - The
n_neighborsparameter default is 20 - The
leaf_sizeparameter default is 30 - The
pparameter is limited top >=1 - The
contaminationparameter must be within the range of 0.0 (not included) to 0.5 (included) - The
contaminationparameter default is 0.1 - Options for the
algorithmparameter include: brute, kd_tree, ball_tree, and auto. The default is auto. - The brute, kd_tree, ball_tree, and auto
algorithmoptions have respective valid metrics. The defaultmetricfor each is minkowski.- Valid metrics for brute include: cityblock, euclidean, l1, l2, manhattan, chebyshev, minkowski, braycurtis, canberra, dice, hamming, jaccard, kulsinski, matching, rogerstanimoto, russellrao, sokalmichener, sokalsneath, cosine, correlation, sqeuclidean, and yule.
- Valid metrics for kd_tree include: cityblock, euclidean, l1, l2, manhattan, chebyshev, and minkowski.
- Valid metrics for ball_tree include: cityblock, euclidean, l1, l2, manhattan, chebyshev, minkowski, braycurtis, canberra, dice, hamming, jaccard, kulsinski, matching, rogerstanimoto, russellrao, sokalmichener, and sokalsneath.
- The output for LocalOutlierFactor is a list of labels titled
is_outlier, assigned1for outliers, and-1for inliers
Syntax
fit LocalOutlierFactor <fields> [n_neighbors=<int>] [leaf_size=<int>] [p=<int>] [contamination=<float>] [metric=<str>] [algorithm=<str>] [anomaly_score=<true|false>]
Syntax constraints
- You cannot save LocalOutlierFactor models using the
intokeyword. This algorithm does not support saving models and you cannot apply a saved model to new data. - LOF does not include the
predictmethod.
Example
The following example uses LocalOutlierFactor on a test set.
| inputlookup iris.csv | fit LocalOutlierFactor petal_length petal_width n_neighbors=10 algorithm=kd_tree metric=minkowski p=1 contamination=0.14 leaf_size=10
MultivariateOutlierDetection
MultivariateOutlierDetection accepts a multivariate dataset. The algorithm receives multiple fields as input, then runs StandardScaler on the multivariate dataset to scale the dataset. Then PCA runs on the scaled dataset, deriving the first principle component (PC_1). Finally the algorithm runs DensityFunction on the single component (PC_1) and returns outliers.
Parameters
The following is a selection of parameters for MultivariateOutlierDetection. The full parameters described in the DensityFunction algorithm all apply to MultivariateOutlierDetection.
- The
partial_fitparameter controls whether an existing model should be incrementally updated on not. This allows you to update an existing model using only new data without having to retrain it on the full training data set.- The
partial_fitparameter default is False. - If
partial_fitis not specified, the model specified is created and replaces the pre-trained model if one exists.
- The
- Using
partial_fit=Trueon an existing model ignores the newly supplied parameters. The parameters supplied at model creation are used instead. - Use the
exclude_distparameter to exclude a minimum of 1 and a maximum of 3 of the available dist parameter values (norm, expon, gaussian_kde, beta).- The
exclude_distparameter is only available when the dist parameter isauto. - DensityFunction will run using any non-excluded dist parameter values.
- Use a comma to note multiple excluded dist parameter values. For example,
exclude_dist="beta,expon" - Attempts to use the
exclude_distparameter on more than 3 dist parameter values, or on a dist parameter other thanautowill result in an error message.
- The
- The
sampleparameter can be used duringfitorapplystages. - The
sampleparameter default is False. - If the
sampleparameter is set to True during thefitstage, the size of the samples will be equal to the training dataset. - If the
sampleparameter is set to True during theapplystage, the size of the samples will be equal to the testing dataset. - If the
sampleparameter is set to True:- Samples are taken from the fitted density function.
- Results output in a new column called
SampledValue. - Sampled values only come from the inlier region of the distribution.
- The
full_sampleparameter can be used duringfitorapplystages. - The
full_sampleparameter default is False. - If the
full_sampleparameter is set to True during the fit stage, the size of the samples will be equal to the training dataset. - If the
full_sampleparameter is set to True during the apply stage, the size of the samples will be equal to the testing dataset. - If the
full_sampleparameter is set to True:- Samples are taken from the fitted density function.
- Results output in a new column called
FullSampledValue. - Sampled values come from the whole distribution (both inlier and outlier regions).
- Use the
summarycommand to inspect the model.- The values reported for the mean and standard deviation are either the statistics of the fitted distribution, or of the data, depending on the type of the distribution.
- In the case of parametric distributions (Normal, Beta, and Exponential) the mean and standard deviation are calculated from the fitted distribution. When the parametric distribution is not a good fit for the data, the reported mean and std might not be close to that of data.
- In the case of non-parametric distributions (Gaussian KDE) the mean and standard deviation are calculated from the data passed in during
fit.
- Version 4.4.0 and higher of MLTK support min and max values in
summary.- The
minvalue is the minimum value of the dataset on which the density function is fitted. - The
maxvalue is the maximum value of the dataset on which the density function is fitted.
- The
- The output for
BoundaryRangesis the boundary ranges of outliers on the density function which are set according to the values of thethresholdparameter. - Each boundary region has three values: boundary opening point, boundary closing point, and percentage of boundary region.
- The boundary region syntax follows the convention of a multi-value field where each boundary region appears in a new line.
- When multiple thresholds are provided, Boundary Ranges for each threshold appears in a different column separated with the suffix of
_th=and the threshold value. - In cases of a single boundary region, the value for the percentage of boundary region is equal to the
thresholdparameter value. - In some distributions (for example Gaussian KDE), the sum of outlier areas might not add up to the exact value of
thresholdparameter value, but will be a close approximation. BoundaryRangesis calculated as an approximation and will be empty in the following two cases:- Where the density function has a sharp peak from low standard deviation.
- When there are a low number of data points.
- Data points that are exactly at the boundary opening or closing point are assigned as inliers. An opening or closing point is determined by the density function in use.
- Normal density function has left and right boundary regions. Data points on the left of the left boundary closing point, and data points on the right of the right boundary opening point are assigned as outliers.
- Exponential density function has one boundary region. Data points on the right of the right boundary opening point are assigned as outliers.
- Beta density function has one boundary region. Data points on the left of the left boundary closing point are assigned as outliers.
- Gaussian KDE density function can have one or more boundary regions, depending on the number of peaks and dips within the density function. Data points in these boundary regions are assigned as outliers. In cases of boundary regions to the left or right, guidelines from Normal density function apply. As the shape for Gaussian KDE density function can differ from dataset to dataset, you do not consistently observe left and right boundary regions.
Syntax
| fit MultivariateOutlierDetection <field1> <field2> ... <fieldN> [by "<field1>[,<field2>,....<field5>]"] [into <model name>] [dist=<str>] [show_density=true|false] [sample=true|false][full_sample=true|false][threshold=<float>|lower_threshold=<float>|upper_threshold=<float>] [metric=<str>] [random_state=<int>] [partial_fit=<true|false>]
You can apply the saved model to new data with the apply command. You can inspect the model learned by MultivariateOutlierDetection with the summary command.
Syntax constraints
The constraints described in the DensityFunction algorithm all apply to MultivariateOutlierDetection.
Examples
The following example shows MultivariateOutlierDetection on a dataset with the fit command.
| inputlookup disk_failures.csv | fit MultivariateOutlierDetection SMART_1_Raw SMART_2_Raw SMART_3_Raw SMART_4_Raw by Model threshold=0.02 into mymultivariateoutliermodel
The following example shows MultivariateOutlierDetection on a dataset with the apply command.
| inputlookup disk_failures.csv | apply mymultivariateoutliermodel show_density=True sample=True
The following example shows MultivariateOutlierDetection on a dataset with the summary command.
| summary mymultivariateoutliermodel
OneClassSVM
The OneClassSVM algorithm uses the scikit-learn OneClassSVM to fit a model from a set of features or fields for detecting anomalies and outliers, where features are expected to contain numerical values. OneClassSVM is an unsupervised outlier detection method.
For further information, see the sci-kit learn documentation: http://scikit-learn.org/stable/modules/svm.html#kernel-functions
Parameters
- The
kernelparameter specifies the kernel type for using in the algorithm, where the default value is kernel isrbf.- Kernel types include: linear, rbf, poly, and sigmoid.
- You can specify the upper bound on the fraction of training error as well as the lower bound of the fraction of support vectors using the
nuparameter, where the default value is 0.5. - The
degreeparameter is ignored by all kernels except the polynomial kernel, where the default value is 3. gammais the kernel co-efficient that specifies how much influence a single data instance has, where the default value is1/ number of features.- The independent term of
coef0in the kernel function is only significant if you have polynomial or sigmoid function. - The term
tolis the tolerance for stopping criteria. - The
shrinkingparameter determines whether to use the shrinking heuristic.
Syntax
fit OneClassSVM <fields> [into <model name>] [kernel=<str>] [nu=<float>] [coef0=<float>] [gamma=<float>] [tol=<float>] [degree=<int>] [shrinking=<true|false>]
- You can save OneClassSVM models using the
intokeyword. - You can apply the saved model later to new data with the
applycommand.
Syntax constraints
- After running the
fitorapplycommand, a new field namedisNormalis generated. This field defines whether a particular record (row) is normal (isNormal=1) or anomalous (isNormal=-1). - You cannot inspect the model learned by OneClassSVM with the
summarycommand.
Example
The following example uses OneClassSVM on a test set.
... | fit OneClassSVM * kernel="poly" nu=0.5 coef0=0.5 gamma=0.5 tol=1 degree=3 shrinking=f into TESTMODEL_OneClassSVM
Classifiers
Classifier algorithms predict the value of a categorical field.
The kfold cross-validation command can be used with all Classifier algorithms. For details, see K-fold cross-validation.
AutoPrediction
AutoPrediction automatically determines the data type as categorical or numeric. AutoPrediction then invokes the RandomForestClassifier algorithm to carry out the prediction. For further details, see RandomForestClassifier. AutoPrediction also executes the data split for training and testing during the fit process, eliminating the need for a separate command or macro. AutoPrediction uses particular cases to determine the data type, and uses the train_test_split function from sklearn to perform the data split.
Parameters
- Use the
target_typeparameter to specify the target field as numeric or categorical. - The
target_typeparameter default is auto. When auto is used, AutoPrediction automatically determines the target field type. - AutoPrediction uses the following data types to determine the
target_typefield as categorical:- Data of type
bool,str, ornumpy.object - Data of type
intand thecriterionoption is specified
- Data of type
- AutoPrediction determines the
target_typefield as numeric for all other cases. - The
test_split_ratiospecifies the splitting of data for model training and model validation. Value must be a float between 0 (inclusive) and 1 (exclusive). - The
test_split_ratiodefault is 0. A value of 0 means all data points get used to train the model.- A
test_split_ratiovalue of 0.3, for example, means 30% for the data points get used for testing and 70% are used for training.
- A
- Use
n_estimatorsto optionally specify the number of trees. - Use
max_depthto optionally set the maximum depth of the tree. - Specify the
criterionvalue for classification (categorical) scenarios. - Ignore the
criterionvalue for regression (numeric) scenarios.
Syntax
fit AutoPrediction Target from Predictors* into PredictorModel target_type=<auto|numeric|categorical> test_split_ratio=<[0-1]>[n_estimators=<int>] [max_depth=<int>] [criterion=<gini | entropy>] [random_state=<int>][max_features=<str>] [min_samples_split=<int>] [max_leaf_nodes=<int>]
You can save AutoPrediction models using the into keyword and apply the saved model later to new data using the apply command.
... | apply PredictorModel
You can inspect the model learned by AutoPrediction with the summary command.
.... | summary PredictorModel
Syntax constraints
- AutoPrediction does not support
partial_fit. - Classification performance output columns for accuracy, f1, precision, and recall only appear if the
target_typeis categorical. - Regression performance output columns for RMSE and rSquared only appear if the
target_typeis numeric.
Example
The following example uses AutoPrediction on a test set.
BernoulliNB
The BernoulliNB algorithm uses the scikit-learn BernoulliNB estimator to fit a model to predict the value of categorical fields where explanatory variables are assumed to be binary-valued. BernoulliNB is an implementation of the Naive Bayes classification algorithm. This algorithm supports incremental fit.
Parameters
- The
alphaparameter controls Laplace/ Lidstone smoothing. The default value is 1.0. - The
binarizeparameter is a threshold that can be used for converting numeric field values to the binary values expected by BernoulliNB. The default value is 0.- If
binarize=0is specified, the default, values > 0 are assumed to be 1, and values <= 0 are assumed to be 0.
- If
- The
fit_priorBoolean parameter specifies whether to learn class prior probabilities. The default value is True. Iffit_prior=fis specified, classes are assumed to have uniform popularity.
Syntax
fit BernoulliNB <field_to_predict> from <explanatory_fields> [into <model name>] [alpha=<float>] [binarize=<float>] [fit_prior=<true|false>] [partial_fit=<true|false>]
You can save BernoulliNB models using the into keyword and apply the saved model later to new data using the apply command.
... | apply TESTMODEL_BernoulliNB
You can inspect the model learned by BernoulliNB with the summary command as well as view the class and log probability information as calculated by the dataset.
.... | summary My_Incremental_Model
Syntax constraints
- The
partial_fitparameter controls whether an existing model should be incrementally updated or not. The default value isFalse, meaning it will not be incrementally updated. Choosingpartial_fit=Trueallows you to update an existing model using only new data without having to retrain it on the full training data set. - Using
partial_fit=Trueon an existing model ignores the newly supplied parameters. The parameters supplied at model creation are used instead. Ifpartial_fit=Falseorpartial_fitis not specified (default is False), the model specified is created and replaces the pre-trained model if one exists. - If
My_Incremental_Modeldoes not exist, the command saves the model data under the model nameMy_Incremental_Model. IfMy_Incremental_Modelexists and was trained using BernoulliNB, the command updates the existing model with the new input. IfMy_Incremental_Modelexists but was not trained by BernoulliNB, an error message displays.
Example
The following example uses BernoulliNB on a test set.
... | fit BernoulliNB type from * into TESTMODEL_BernoulliNB alpha=0.5 binarize=0 fit_prior=f
DecisionTreeClassifier
The DecisionTreeClassifier algorithm uses the scikit-learn DecisionTreeClassifier estimator to fit a model to predict the value of categorical fields. For further information, see the sci-kit learn documentation: http://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html.
Parameters
To specify the maximum depth of the tree to summarize, use the limit argument. The default value for the limit argument is 5.
... | summary model_DTC limit=10
Syntax
fit DecisionTreeClassifier <field_to_predict> from <explanatory_fields> [into <model_name>] [max_depth=<int>] [max_features=<str>] [min_samples_split=<int>] [max_leaf_nodes=<int>] [criterion=<gini|entropy>] [splitter=<best|random>] [random_state=<int>]
You can save DecisionTreeClassifier models by using the into keyword and apply it to new data later by using the apply command.
... | apply model_DTC
You can inspect the decision tree learned by DecisionTreeClassifier with the summary command.
... | summary model_DTC
See a JSON representation of the tree by giving json=t as an argument to the summary command.
... | summary model_DTC json=t
Example
The following example uses DecisionTreeClassifier on a test set.
... | fit DecisionTreeClassifier SLA_violation from * into sla_model | ...
GaussianNB
The GaussianNB algorithm uses the scikit-learn GaussianNB estimator to fit a model to predict the value of categorical fields, where the likelihood of explanatory variables is assumed to be Gaussian. GaussianNB is an implementation of Gaussian Naive Bayes classification algorithm. This algorithm supports incremental fit.
Parameters
- The
partial_fitparameter controls whether an existing model should be incrementally updated or not. This allows you to update an existing model using only new data without having to retrain it on the full training data set. - The
partial_fitparameter default is False.
Syntax
fit GaussianNB <field_to_predict> from <explanatory_fields> [into <model name>] [partial_fit=<true|false>]
You can save GaussianNB models using the into keyword and apply the saved model later to new data using the apply command.
... | apply TESTMODEL_GaussianNB
You can inspect models learned by GaussianNB with the summary command.
... | summary My_Incremental_Model
Syntax constraints
- If
My_Incremental_Modeldoes not exist, the command saves the model data under the model nameMy_Incremental_Model. IfMy_Incremental_Modelexists and was trained using GaussianNB, the command updates the existing model with the new input. IfMy_Incremental_Modelexists but was not trained by GaussianNB, an error message is thrown. - If
partial_fit=Falseorpartial_fitis not specified the model specified is created and replaces the pre-trained model if one exists.
Example
The following example uses GaussianNB on a test set.
... | fit GaussianNB species from * into TESTMODEL_GaussianNB
The following example includes the partial_fit command.
| inputlookup iris.csv | fit GaussianNB species from * partial_fit=true into My_Incremental_Model
GradientBoostingClassifier
This algorithm uses the GradientBoostingClassifier from scikit-learn to build a classification model by fitting regression trees on the negative gradient of a deviance loss function. For further information, see the sci-kit learn documentation: http://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingClassifier.html.
Syntax
fit GradientBoostingClassifier <field_to_predict> from <explanatory_fields>[into <model name>] [loss=<deviance | exponential>] [max_features=<str>] [learning_rate =<float>] [min_weight_fraction_leaf=<float>] [n_estimators=<int>] [max_depth=<int>] [min_samples_split =<int>] [min_samples_leaf=<int>] [max_leaf_nodes=<int>] [random_state=<int>]
You can apply the saved model later to new data using the apply command.
... | apply TESTMODEL_GradientBoostingClassifier
You can inspect features learned by GradientBoostingClassifier with the summary command.
... | summary TESTMODEL_GradientBoostingClassifier
Example
The following example uses GradientBoostingClassifier on a test set.
... | fit GradientBoostingClassifier target from * into TESTMODEL_GradientBoostingClassifier
LogisticRegression
The LogisticRegression algorithm uses the scikit-learn LogisticRegression estimator to fit a model to predict the value of categorical fields.
Parameters
- The
fit_interceptparameter specifies whether the model includes an implicit intercept term. - The default value of the
fit_interceptparameter is True. - The
probabilitiesparameter specifies whether probabilities for each possible field value should be returned alongside the predicted value. - The default value of the
probabilitiesparameter is False.
Syntax
fit LogisticRegression <field_to_predict> from <explanatory_fields> [into <model name>] [fit_intercept=<true|false>] [probabilities=<true|false>]
You can save LogisticRegression models using the into keyword and apply new data later using the apply command.
... | apply sla_model
You can inspect the coefficients learned by LogisticRegression with the summary command.
... | summary sla_model
Example
The following examples uses LogisticRegression on a test set.
... | fit LogisticRegression SLA_violation from IO_wait_time into sla_model | ...
MLPClassifier
The MLPClassifier algorithm uses the scikit-learn Multi-layer Perceptron estimator for classification. MLPClassifier uses a feedforward artificial neural network model that trains using backpropagation. This algorithm supports incremental fit.
For descriptions of the batch_size , random_state and max_iter parameters, see the scikit-learn documentation at http://scikit-learn.org/stable/modules/generated/sklearn.neural_network.MLPClassifier.html
Using the MLPClassifier algorithm requires running version 1.3 or above of the Python for Scientific Computing add-on.
Parameters
- The
partial_fitparameter controls whether an existing model should be incrementally updated on not. This allows you to update an existing model using only new data without having to retrain it on the full training data set. - The
partial_fitparameter default is False. - The
hidden_layer_sizesparameter format (int) varies based on the number of hidden layers in the data.
Syntax
fit MLPClassifier <field_to_predict> from <explanatory_fields> [into <model name>]
[batch_size=<int>] [max_iter=<int>] [random_state=<int>] [hidden_layer_sizes=<int>-<int>-<int>]
[activation=<str>] [solver=<str>] [learning_rate=<str>]
[tol=<float>} {momentum=<float>]
You can save MLPClassifier models by using the into keyword and apply it to new data later by using the apply command.
You can inspect models learned by MLPClassifier with the summary command.
... | summary My_Example_Model
Syntax constraints
- If
My_Example_Modeldoes not exist, the model is saved to it. - If
My_Example_Modelexists and was trained using MLPClassifier, the command updates the existing model with the new input. - If
My_Example_Modelexists but was not trained using MLPClassifier, an error message displays.
Example
The following example uses MLPClassifier on a test set.
... | inputlookup diabetes.csv | fit MLPClassifier response from * into MLP_example_model hidden_layer_sizes='100-100-80' |...
The following example includes the partial_fit command.
| inputlookup iris.csv | fit MLPClassifier species from * partial_fit=true into My_Example_Model
RandomForestClassifier
The RandomForestClassifier algorithm uses the scikit-learn RandomForestClassifier estimator to fit a model to predict the value of categorical fields.
For descriptions of the n_estimators, max_depth, criterion, random_state, max_features, min_samples_split, and max_leaf_nodes parameters, see the scikit-learn documentation at http://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html.
Syntax
fit RandomForestClassifier <field_to_predict> from <explanatory_fields> [into <model name>] [n_estimators=<int>] [max_depth=<int>] [criterion=<gini | entropy>] [random_state=<int>] [max_features=<str>] [min_samples_split=<int>] [max_leaf_nodes=<int>]
You can save RandomForestClassifier models using the into keyword and apply new data later using the apply command.
... | apply sla_model
You can list the features that were used to fit the model, as well as their relative importance or influence with the summary command.
... | summary sla_model
Example
The following example uses RandomForestClassifier on a test set.
... | fit RandomForestClassifier SLA_violation from * into sla_model | ...
SGDClassifier
The SGDClassifier algorithm uses the scikit-learn SGDClassifier estimator to fit a model to predict the value of categorical fields. This algorithm supports incremental fit.
Parameters
- The
partial_fitparameter controls whether an existing model should be incrementally updated or not. This allows you to update an existing model using only new data without having to retrain it on the full training data set. - The
partial_fitparameter default is False. n_iter=<int>is the number of passes over the training data also known as epochs. The default is 5. The number of iterations is set to 1 if usingpartial_fit.- The
loss=<hinge|log|modified_huber|squared_hinge|perceptron>parameter is the loss function to be used.- Defaults to
hinge, which gives a linear SVM.
- Defaults to
- The
logloss gives logistic regression, a probabilistic classifier. modified_huberis another smooth loss that brings tolerance to outliers as well as probability estimates.squared_hingeis like hinge but is quadratically penalized.perceptronis the linear loss used by the perceptron algorithm.- The
fit_intercept=<true|false>parameter specifies whether the intercept should be estimated or not. The default is True. penalty=<l2|l1|elasticnet>is the penalty, also known as regularization term, to be used. The default is l2.learning_rate=<constant|optimal|invscaling>is the learning rate.constant: eta = eta0optimal: eta = 1.0/(alpha * t)invscaling: eta = eta0 / pow(t, power_t)- The default is
invscaling
l1_ratio=<float>is the Elastic Net mixing parameter, with 0 <= l1_ratio <= 1 (default 0.15).- l1_ratio=0 corresponds to L2 penalty, l1_ratio=1 to L1.
alpha=<float>is the constant that multiplies the regularization term (default 0.0001). Also used to compute learning_rate when set tooptimal.eta0=<float>is the initial learning rate. The default is 0.01.power_t=<float>is the exponent for inverse scaling learning rate. The default is 0.25.random_state=<int>is the seed of the pseudo random number generator to use when shuffling the data.
Syntax
fit SGDClassifier <field_to_predict> from <explanatory_fields> [into <model name>] [partial_fit=<true|false>] [loss=<hinge|log|modified_huber|squared_hinge|perceptron>] [fit_intercept=<true|false>] [random_state=<int>] [n_iter=<int>] [l1_ratio=<float>] [alpha=<float>] [eta0=<float>] [power_t=<float>] [penalty=<l1|l2|elasticnet>] [learning_rate=<constant|optimal|invscaling>]
You can save SGDClassifier models using the into keyword and apply the saved model later to new data using the apply command.
... | apply sla_model
You can inspect the model learned by SGDClassifier with the summary command.
... | summary sla_model
Syntax constraints
- If
My_Incremental_Modeldoes not exist, the command saves the model data under the model nameMy_Incremental_Model. - If
My_Incremental_Modelexists and was trained using SGDClassifier, the command updates the existing model with the new input. - If
My_Incremental_Modelexists but was not trained by SGDClassifier, an error displays. - Using
partial_fit=trueon an existing model ignores the newly supplied parameters. The parameters supplied at model creation are used instead. - If
partial_fit=falseorpartial_fitis not specified the model specified is created and replaces the pre-trained model if one exists.
Example
The following example uses SGDClassifier on a test set.
... | fit SGDClassifier SLA_violation from * into sla_model
The following example includes the partial_fit=<true|false> command.
| inputlookup iris.csv | fit SGDClassifier species from * partial_fit=true into My_Incremental_Model
SVM
The SVM algorithm uses the scikit-learn kernel-based SVC estimator to fit a model to predict the value of categorical fields. It uses the radial basis function (rbf) kernel by default. For descriptions of the C and gamma parameters, see the scikit-learn documentation at http://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html.
Kernel-based methods such as the scikit-learn SVC tend to work best when the data is scaled, for example, using our StandardScaler algorithm:
| fit StandardScaler . For details, see ''A Practical Guide to Support Vector Classification'' at https://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide.pdf.
Parameters
- The
gammaparameter controls the width of the rbf kernel. The default value is1 /number of fields. - The
Cparameter controls the degree of regularization when fitting the model. The default value is 1.0.
Syntax
fit SVM <field_to_predict> from <explanatory_fields> [into <model name>] [C=<float>] [gamma=<float>]
You can save SVM models using the into keyword and apply new data later using the apply command.
... | apply sla_model
Syntax constraints
You cannot inspect the model learned by SVM with the summary command.
Example
The following example uses SVM on a test set.
... | fit SVM SLA_violation from * into sla_model | ...
Clustering Algorithms
Clustering is the grouping of data points. Results will vary depending upon the clustering algorithm used. Clustering algorithms differ in how they determine if data points are similar and should be grouped. For example, the K-means algorithm clusters based on points in space, whereas the DBSCAN algorithm clusters based on local density.
Birch
The Birch algorithm uses the scikit-learn Birch clustering algorithm to divide data points into set of distinct clusters. The cluster for each event is set in a new field named cluster. This algorithm supports incremental fit.
Parameters
- The
kparameter specifies the number of clusters to divide the data into after the final clustering step, which treats the sub-clusters from the leaves of the CF tree as new samples.- By default, the cluster label field name is
cluster. Change that behavior by using theaskeyword to specify a different field name.
- By default, the cluster label field name is
- The
partial_fitparameter controls whether an existing model should be incrementally updated on not. This allows you to update an existing model using only new data without having to retrain it on the full training data set. - The
partial_fitparameter default is False.
Syntax
fit Birch <fields> [into <model name>] [k=<int>][partial_fit=<true|false>] [into <model name>]
You can save Birch models using the into keyword and apply new data later using the apply command.
... | apply Birch_model
Syntax constraints
- If
My_Incremental_Modeldoes not exist, the command saves the model data under the model nameMy_Incremental_Model. - If
My_Incremental_Modelexists and was trained using Birch, the command updates the existing model with the new input. - If
My_Incremental_Modelexists but was not trained by Birch, an error message displays. - Using
partial_fit=trueon an existing model ignores the newly supplied parameters. The parameters supplied at model creation are used instead. - If
partial_fit=falseorpartial_fitis not specified the model specified is created and replaces the pre-trained model if one exists. - You cannot inspect the model learned by Birch with the
summarycommand.
Examples
The following example uses Birch on a test set.
... | fit Birch * k=3 | stats count by cluster
The following example includes the partial_fit command.
| inputlookup track_day.csv | fit Birch * k=6 partial_fit=true into My_Incremental_Model
DBSCAN
The DBSCAN algorithm uses the scikit-learn DBSCAN clustering algorithm to divide a result set into distinct clusters. The cluster for each event is set in a new field named cluster. DBSCAN is distinct from K-Means in that it clusters results based on local density, and uncovers a variable number of clusters, whereas K-Means finds a precise number of clusters. For example, k=5 finds 5 clusters.
Parameters
- The
epsparameter specifies the maximum distance between two samples for them to be considered in the same cluster.- By default, the cluster label field name is
cluster. Change that behavior by using theaskeyword to specify a different field name.
- By default, the cluster label field name is
- The
min_samplesparameter defines the number of samples, or the total weight, in a neighborhood for a point to be considered as a core point - including the point itself. You can choose themin_samplesparameter's best value based on preference for cluster density or noise in your dataset. - The
min_samplesparameter is optional. - The
min_samplesdefault value is 5. - The minimum value for the
min_samplesparameter is 3. - If
min_samples=8you need at least 8 data points to form a dense cluster.
If you choose the min_samples parameter's best value based on noise in your dataset, it's recommended to have a larger data set to pull from.
Syntax
| fit DBSCAN <fields> [eps=<number>] [min_samples=<integer>]
Syntax constraints
You cannot save DBSCAN models using the into keyword. To predict cluster assignments for future data, combine the DBSCAN algorithm with any classifier algorithm. For example, first cluster the data using DBSCAN, then fit RandomForestClassifier to predict the cluster.
Examples
The following example uses DBSCAN without the min_samples parameter.
... | fit DBSCAN * | stats count by cluster
The following example uses DBSCAN with the min_samples parameter.
...| inputlookup track_day.csv | fit DBSCAN eps=0.5 min_samples=1000 speed | table speed cluster
G-means
G-means is a clustering algorithm based on K-means. The G-means algorithm is similar in purpose to the X-means algorithm. G-means uses the Anderson-Darling statistical test to determine when to split a cluster.
Using the G-means algorithm has the following advantages:
- The parameter
kis computed automatically - G-means can produce more accurate clusters than X-means in some real-world scenarios
Parameters
- The cluster splitting decision is done using the Anderson-Darling statistical test.
- The cluster for each event is set in a new field named cluster, and the total number of clusters is set in a new field named
n_clusters. - By default, the cluster label field name is
cluster.- You can change the default behavior by using the
askeyword to specify a different field name.
- You can change the default behavior by using the
- Optionally use the
random_stateparameter to set a seed value.random_statemust be an integer.
Syntax
| fit GMeans <fields> [into <cluster_model>]
You can apply new data to the saved G-means model using the apply command.
... | apply cluster_model
You can save G-means models using the into command. You can inspect the model learned by G-means with the summary command.
...| summary cluster_model
Example
The following example uses G-means on a test set.
| inputlookup housing.csv | fields median_house_value distance_to_employment_center crime_rate | fit GMeans * random_state=42 into cluster_model
K-means
K-means clustering is a type of unsupervised learning. It is a clustering algorithm that groups similar data points, with the number of groups represented by the variable k. The K-means algorithm uses the scikit-learn K-means implementation. The cluster for each event is set in a new field named cluster. Use the K-means algorithm when you have unlabeled data and have at least approximate knowledge of the total number of groups into which the data can be divided.
Using the K-means algorithm has the following advantages:
- Computationally faster than most other clustering algorithms.
- Simple algorithm to explain and understand.
- Normally produces tighter clusters than hierarchical clustering.
Using the K-means algorithm has the following disadvantages:
- Difficult to determine optimal or true value of
k. See X-means. - Sensitive to scaling. See StandardScaler.
- Each clustering may be slightly different, unless you specify the
random_stateparameter. - Does not work well with clusters of different sizes and density.
For descriptions of default value of K, see the scikit-learn documentation at http://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html
Parameters
The k parameter specifies the number of clusters to divide the data into. By default, the cluster label field name is cluster. Change that behavior by using the as keyword to specify a different field name.
Syntax
fit KMeans <fields> [into <model name>] [k=<int>] [random_state=<int>]
You can save K-means models using the into keyword when using the fit command.
You can apply the model to new data using the apply command.
... | apply cluster_model
You can inspect the model using the summary command.
... | summary cluster_model
Example
The following example uses K-means on a test set.
... | fit KMeans * k=3 | stats count by cluster
SpectralClustering
The SpectralClustering algorithm uses the scikit-learn SpectralClustering clustering algorithm to divide a result set into set of distinct clusters. SpectralClustering first transforms the input data using the Radial Basis Function (rbf) kernel, and then performs K-Means clustering on the result. Consequently, SpectralClustering can learn clusters with a non-convex shape. The cluster for each event is set in a new field named cluster.
Parameters
The k parameter specifies the number of clusters to divide the data into after kernel step. By default, the cluster label field name is cluster. Change that behavior by using the as keyword to specify a different field name.
Syntax
fit SpectralClustering <fields> [k=<int>] [gamma=<float>] [random_state=<int>]
Syntax constraints
You cannot save SpectralClustering models using the into keyword. If you want to be able to predict cluster assignments for future data, you can combine the SpectralClustering algorithm with any clustering algorithm. For example, first cluster the data using SpectralClustering, then fit a classifier to predict the cluster using RandomForestClassifier.
Example
The following example uses SpectralClustering on a test set.
... | fit SpectralClustering * k=3 | stats count by cluster
X-means
Use the X-means algorithm when you have unlabeled data and no prior knowledge of the total number of labels into which that data could be divided. The X-means clustering algorithm is an extended K-means that automatically determines the number of clusters based on Bayesian Information Criterion (BIC) scores. Starting with a single cluster, the X-means algorithm goes into action after each run of K-means, making local decisions about which subset of the current centroids should split themselves in order to fit the data better.
Using the X-means algorithm has the following advantages:
- Eliminates the requirement of having to provide the value of
k. - Normally produces tighter clusters than hierarchical clustering.
Using the X-means algorithm has the following disadvantages:
- Sensitive to scaling. See StandardScaler.
- Different initializations might result in different final clusters.
- Does not work well with clusters of different sizes and density.
Parameters
- The splitting decision is done by computing the BIC.
- The cluster for each event is set in a new field named cluster, and the total number of clusters is set in a new field named
n_clusters. - By default, the cluster label field name is
cluster.- You can change the default behavior by using the
askeyword to specify a different field name.
- You can change the default behavior by using the
Syntax
fit XMeans <fields> [into <model name>]
You can apply new data to the saved X-means model using the apply command.
... | apply cluster_model
You can save X-means models using the into command. You can inspect the model learned by X-means with the summary command.
...| summary cluster_model
Example
The following example uses X-means on a test set.
... | fit XMeans * | stats count by cluster
Cross-validation
Cross-validation assesses how well a statistical model generalizes on an independent dataset. Cross-validation tells you how well your machine learning model is expected to perform on data that it has not been trained on. There are many types of cross-validation, but K-fold cross-validation (kfold_cv) is one of the most common.
Cross-validation is typically used for the following machine learning scenarios:
- Comparing two or more algorithms against each other for selecting the best choice on a particular dataset.
- Comparing different choices of hyper-parameters on the same algorithm for choosing the best hyper-parameters for a particular dataset.
- An improved method over a train/test split for quantifying model generalization.
Cross-validation is not well suited for time-series charts:
- In situations where the data is ordered such as time-series, cross-validation is not well suited because the training data is shuffled. In these situations, other methods such as Forward Chaining are more suitable.
- The most straightforward implementation is to wrap sklearn's Time Series Split. Learn more here: https://en.wikipedia.org/wiki/Forward_chaining
K-fold cross-validation
In the kfold_cv parameter, the training set is randomly partitioned into k equal-sized subsamples. Then, each sub-sample takes a turn at becoming the validation (test) set, predicted by the other k-1 training sets. Each sample is used exactly once in the validation set, and the variance of the resulting estimate is reduced as k is increased. The disadvantage of the kfold_cv parameter is that k different models have to be trained, leading to long execution times for large datasets and complex models.
The scores obtained from K-fold cross-validation are generally a less biased and less optimistic estimate of the model performance than a standard training and testing split.
You can obtain k performance metrics, one for each training and testing split. These k performance metrics can then be averaged to obtain a single estimate of how well the model generalizes on unseen data.
Syntax
The kfold_cv parameter is applicable to to all classification and regression algorithms, and you can append the command to the end of an SPL search.
Here kfold_cv=<int> specifies that k=<int> folds is used. When you specify a classification algorithm, stratified k-fold is used instead of k-fold. In stratified k-fold, each fold contains approximately the same percentage of samples for each class.
..| fit <classification | regression algo> <targetVariable> from <featureVariables> [options] kfold_cv=<int>
The kfold_cv parameter cannot be used when saving a model.
Output
The kfold_cv parameter returns performance metrics on each fold using the same model specified in the SPL - including algorithm and hyper parameters. Its only function is to give you insight into how well you model generalizes. It does not perform any model selection or hyper parameter tuning.
Examples
The first example shows the kfold_cv parameter used in classification. Where the output is a set of metrics for each fold including accuracy, f1_weighted, precision_weighted, and recall_weighted.
This second example shows the kfold_cv parameter used in classification. Where the output is a set of metrics for each the neg_mean_squared_error and r^2 folds.
Feature Extraction
Feature extraction algorithms transform fields for better prediction accuracy.
FieldSelector
The FieldSelector algorithm uses the scikit-learn GenericUnivariateSelect to select the best predictor fields based on univariate statistical tests. For descriptions of the mode and param parameters, see the scikit-learn documentation at http://scikit-learn.org/stable/modules/generated/sklearn.feature_selection.GenericUnivariateSelect.html.
Parameters
The type parameter specifies if the field to predict is categorical or numeric.
Syntax
fit FieldSelector <field_to_predict> from <explanatory_fields> [into <model name>] [type=<categorical, numeric>] [mode=<k_best, fpr, fdr, fwe, percentile>] [param=<int>]
You can save FieldSelector models using the into keyword and apply new data later using the apply command.
... | apply sla_model
You can inspect the model learned by FieldSelector with the summary command.
| summary sla_model
Example
The following example uses FieldSelector on a test set.
... | fit FieldSelector type=categorical SLA_violation from * into sla_model | ...
HashingVectorizer
The HashingVectorizer algorithm converts text documents to a matrix of token occurrences. It uses a feature hashing strategy to allow for hash collisions when measuring the occurrence of tokens. It is a stateless transformer, meaning that it does not require building a vocabulary of the seen tokens. This reduces the memory footprint and allows for larger feature spaces.
HashingVectorizer is comparable with the TFIDF algorithm, as they share many of the same parameters. However HashingVectorizer is a better option for building models with large text fields provided you do not need to know term frequencies, and only want outcomes.
For descriptions of the ngram_range, analyzer, norm, and token_pattern parameters, see the scikit-learn documentation at https://scikit-learn.org/0.19/modules/generated/sklearn.feature_extraction.text.HashingVectorizer.html
Parameters
- The
reduceparameter is eitherTrueorFalseand determines whether or not to reduce the output to a smaller dimension using TruncatedSVD. - The
reduceparameter default is True. - The
k=<int>parameter sets the number of dimensions to reduce when thereduceparameter is set totrue. Default is 100. - The default for the
max_featuresparameter is 10,000. - The
n_itersparameter specifies the number of iterations to to use when performing dimensionality reduction. This is only used when thereduceparameter is set toTrue. Default is 5.
Syntax
fit HashingVectorizer <field_to_convert> [max_features=<int>] [n_iters=<int>] [reduce=<bool>] [k=<int>] [ngram_range=<int>-<int>] [analyzer=<str>] [norm=<str>] [token_pattern=<str>] [stop_words=english]
Syntax constraints
HashingVectorizer does not support saving models, incremental fit, or K-fold cross validation.
Example
The following example uses HashingVectorizer to hash the text dataset and applies KMeans clustering (where k=3) on the hashed fields.
| inputlookup authorization.csv | fit HashingVectorizer Logs ngram_range=1-2 k=50 stop_words=english | fit KMeans Logs_hashed* k=3 | fields cluster* Logs | sample 5 by cluster | sort by cluster
ICA
ICA (Independent component analysis) separates a multivariate signal into additive sub-components that are maximally independent. Typically, ICA is not used for separating superimposed signals, but for reducing dimensionality. The ICA model does not include a noise term for the model to be correct, meaning whitening must be applied. Whitening can be done internally using the whiten argument, or manually using one of the PCA variants.
Parameters
- The
n_componentsparameters determines the number of components ICA uses. - The
n_componentsparameter is optional. - The
n_componentsparameter default isNone. IfNoneis selected, all components are used. - Use the
algorithmparameter to applyparallelordeflationalgorithm for FastICA. - The the
algorithmparameter default isalgorithm='parallel'. - Use the
whitenparameter to set a noise term. - The
whitenparameter is optional. - If the
whitenparameter isFalseno whitening is performed. - The
whitenparameter default isTrue. - The
max_iterparameter determines the maximum number of iterations during the running of thefitcommand. - The
max_iterparameter is optional. - The
max_iterparameter default is 200. - The
funparameter determines the functional form of the G function used in the approximation to neg-entropy. - The
funparameter is optional. - The
funparameter default islogcosh. Other options for this parameter areexporcube. - The
tolparameter sets the tolerance on update at each iteration. - The
tolparameter is optional. - The
tolparameter default is 0.0001 . - The
random_stateparameter sets the seed value used by the random number generator. - The
random_stateparameter default isNone. - If
random_state=Nonethen a random seed value is used.
Syntax
fit ICA n_components=<int>, algorithm=<"parallel"|"deflation">, whiten=<bool>, fun=<"logcosh"|"exp"|"cube">, max_iter=<int>, tol=<float>, random_state=<int> <explanatory_fields> [into <model name>]
You can save ICA models using the into keyword and apply new data later using the apply command.
Syntax constraints
You cannot inspect the model learned by ICA with the summary command.
Example
The following example shows how ICA is able to find the two original sources of data from two measurements that have mixes of both. As a comparison, PCA is used to show the difference between the two – PCA is not able to identify the original sources.
| makeresults count=2 | streamstats count as count | eval time=case(count=2,relative_time(now(),"+2d"),count=1,now()) | makecontinuous time span=15m | eval _time=time | eval s1 = sin(2*time) | eval s2 = sin(4*time) | eval m1 = 1.5*s1 + .5*s2, m2 = .1*s1 + s2 | fit ICA m1, m2 n_components=2 as IC | fit PCA m1, m2 k=2 as PC | fields _time, * | fields - count, time
KernelPCA
The KernelPCA algorithm uses the scikit-learn KernelPCA to reduce the number of fields by extracting uncorrelated new features out of data. The difference between KernelPCA and PCA is the use of kernels in the former, which helps with finding nonlinear dependencies among the fields. Currently, KernelPCA only supports the Radial Basis Function (rbf) kernel.
For descriptions of the gamma, degree, tolerance, and max_iteration parameters, see the scikit-learn documentation at http://scikit-learn.org/stable/modules/generated/sklearn.decomposition.KernelPCA.html.
Kernel-based methods such as KernelPCA tend to work best when the data is scaled, for example, using our StandardScaler algorithm: | fit StandardScaler . For details, see ''A Practical Guide to Support Vector Classification'' at https://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide.pdf.
Parameters
The k parameter specifies the number of features to be extracted from the data. The other parameters are for fine tuning of the kernel.
Syntax
fit KernelPCA <fields> [into <model name>] [degree=<int>] [k=<int>] [gamma=<int>] [tolerance=<int>] [max_iteration=<int>]
You can save KernelPCA models using the into keyword and apply new data later using the apply command.
... | apply user_feedback_model
Syntax constraints
You cannot inspect the model learned by KernelPCA with the summary command.
Example
The following example uses KernelPCA on a test set.
... | fit KernelPCA * k=3 gamma=0.001 | ...
NPR
The Normalized Perlich Ratio (NPR) algorithm converts high cardinality categorical field values into numeric field entries while intelligently handling space optimization. NPR offers low computational costs to perform feature extraction on variables with high cardinalities such as ZIP codes or IP addresses.
NPR does not perform one-hot encoding unlike other algorithms that leverage the fit and apply commands.
Parameters
- Use the
summarycommand to inspect the variance information of the saved model. - After running NPR the transformed dataset has calculated ratios for all feature variables (
feature_field). Based on the training data NPR calculates a variable ofX_unobservedwhich can be used as a replacement value in the following two scenarios:- In conjunction with the
fitcommand NPR initially replaces missing values in the dataset forfeature_fieldwith the keywordunobservedwhich is then replaced by the calculated NPR value ofX_unobserved. - In conjunction with the
applycommand, any new value fortarget_fieldthat was not visible during model training but is encountered in the test dataset.
- In conjunction with the
- The number of transformed columns created after running NPR is equal to the number of distinct values for
feature_fieldwithin the search string. - From the saved model, use the
varianceoutput field to examine the contribution of a particular feature towards the accuracy of the prediction. Higher variance indicates highly important categorical values whereas low variance indicates the value being of lower importance towards the target prediction. Variance may assist in the process of discarding irrelevant feature variables.
Syntax
fit NPR <target_field> from <feature_field> [into <model name>]
You can couple NPR with existing MLTK algorithms to feed the transformed results to the model as a means to enhance predictions.
| fit NPR <target_field> from <feature_field> | fit SGDClassifier <target_field> from NPR
You can save NPR models using the into keyword and apply new data later using the apply command.
| input lookup disk_failures.csv | tail 1000 | apply npr_disk
You can inspect the model learned by NPR with the summary command.
| summary npr_disk
Syntax constraints
- The wildcard (*) character is not supported.
- The maximum matrix size calculated from |X| * |Y| where X is the feature_field and Y is the target_field is 10000000. For example, if number of distinct categorical feature values are 1000 and distinct categorical target values are 100 then the matrix size is 100000.
Examples
The following example uses NPR on a test set.
| inputlookup disk_failures.csv| head 5000 | fit NPR DiskFailure from Model into npr_disk
The following example couples NPR with another MLTK algorithm on a test set.
| inputlookup disk_failures.csv| head 5000 | fit NPR DiskFailure from Model | fit SGDClassifier DiskFailure from NPR_* random_state=42 n_iter=2 | score accuracy_score DiskFailure against predicted*
The following example uses NPR over multiple fields with additional uses of the fit command.
| inputlookup disk_failures.csv | head 5000 | fit NPR DiskFailure from Model into npr_disk_1 | fit NPR DiskFailure from SerialNumber into npr_disk_2
PCA
The Principal Component Analysis (PCA) algorithm uses the scikit-learn PCA algorithm to reduce the number of fields by extracting new, uncorrelated features out of the data.
Parameters
- The
kparameter specifies the number of features to be extracted from the data. - The
varianceparameter is short for percentage variance ratio explained. This parameter determines the percentage of variance ratio explained in the principal components of the PCA. It computes the number of principal components dynamically by preserving the specified variance ratio. - The
varianceparameter defaults to 1 if k is not provided. - The
varianceparameter can take a value between 0 and 1. - The
explained_varianceparameter measures the proportion to which the principal component accounts for dispersion of a given dataset. A higher value denotes a higher variation. - The
explained_variance_ratioparameter is the percentage of variance explained by each of the selected components.
Syntax
fit PCA <fields> [into <model name>] [k=<int>] [variance=<float>]
You can save PCA models using the into keyword and apply new data later using the apply command.
...into example_hard_drives_PCA_2 | apply example_hard_drives_PCA_2
You can inspect the model learned by PCA with the summary command.
| summary example_hard_drives_PCA_2
Syntax constraints
The variance parameter and k parameter cannot be used together. They are mutually exclusive.
Examples
The following example uses PCA on a test set.
| fit PCA "SS_SMART_1_Raw", "SS_SMART_2_Raw", "SS_SMART_3_Raw", "SS_SMART_4_Raw", "SS_SMART_5_Raw" k=2 into example_hard_drives_PCA_2
The following example includes the variance parameter. The value variance=0.5 tells the algorithm to choose as many principal components for the data set until able to explain 50% of the variance in the original dataset.
| fit PCA "SS_SMART_1_Raw", "SS_SMART_2_Raw", "SS_SMART_3_Raw", "SS_SMART_4_Raw", "SS_SMART_5_Raw" variance=0.50 into example_hard_drives_PCA_2
TFIDF
The TFIDF algorithm uses the scikit-learn TfidfVectorizer to convert raw text data into a matrix making it possible to use other machine learning estimators on the data. For descriptions of max_df, min_df, ngram_range, analyzer, norm, and token_pattern parameters, see the scikit-learn documentation at http://scikit-learn.org/stable/modules/generated/sklearn.feature_extraction.text.TfidfVectorizer.html.
TFIDF uses memory to create a dictionary of all terms including ngrams and words, and expands the Splunk search events with additional fields per event. If you are concerned with memory limits, consider using the HashingVectorizer algorithm.
Parameters
To configure the algorithm to ignore common English words (for example, "the", "it", "at", and "that"), set stop_words to english. For other languages (for example, machine language) you can ignore the common words by setting max_df to a value greater than or equal to 0.7 and less than 1.0.
Syntax
fit TFIDF <field_to_convert> [into <model name>] [max_df=<int>] [min_df=<int>] [ngram_range=<int>-<int>] [analyzer=<str>] [norm=<str>] [token_pattern=<str>] [stop_words=english]
You can save TFIDF models using the into keyword and apply new data later using the apply command.
... | apply user_feedback_model
Syntax constraints
You cannot inspect the model learned by TFIDF with the summary command.
Example
The following example uses TFIDF to convert the text dataset to a matrix of TF-IDF features and then applies KMeans clustering (where k=3) on the matrix.
| inputlookup authorization.csv | fit TFIDF Logs ngram_range=1-2 ngram_range=1-2 max_df=0.6 min_df=0.2 stop_words=english | fit KMeans Logs_tfidf* k=3 | fields cluster Logs | sample 6 by cluster | sort by cluster
Preprocessing (Prepare Data)
Preprocessing algorithms are used for preparing data. Other algorithms can also be used for preprocessing that may not be organized under this section. For example, PCA can be used for both Feature Extraction and Preprocessing.
Imputer
The Imputer algorithm is a preprocessing step wherein missing data is replaced with substitute values. The substitute values can be estimated, or based on other statistics or values in the dataset. To use Imputer, the user passes in the names of the fields to impute, along with arguments specifying the imputation strategy, and the values representing missing data. Imputer then adds new imputed versions of those fields to the data, which are copies of the original fields, except that their missing values are replaced by values computed according to the imputation strategy.
Parameters
- Available imputation strategies include mean, median, most frequent, and field. The default strategy is
mean. - All but the
fieldparameter require numeric data. Thefieldstrategy accepts categorical data.
Syntax
.. | fit Imputer <field>* [as <field prefix>] [missing_values=<"NaN"|integer>] [strategy=<mean|median|most_frequent>] [into <model name>]
You can inspect the value (mean, median, or mode) that was substituted for missing values by Imputer with the summary command.
... | summary <imputer model name>
You can save Imputer models using the into keyword and apply new data later using the apply command.
... | apply <imputer model name>
Example
The following example uses Imputer on a test set.
| inputlookup server_power.csv | eval ac_power_missing=if(random() % 3 = 0, null, ac_power) | fields - ac_power | fit Imputer ac_power_missing | eval imputed=if(isnull(ac_power_missing), 1, 0) | eval ac_power_imputed=round(Imputed_ac_power_missing, 1) | fields - ac_power_missing, Imputed_ac_power_missing
RobustScaler
The RobustScaler algorithm uses the scikit-learn RobustScaler algorithm to standardize data fields by scaling their median and interquartile range to 0 and 1, respectively. It is very similar to the StandardScaler algorithm, in that it helps avoid dominance of one or more fields over others in subsequent machine learning algorithms, and is practically required for some algorithms, such as KernelPCA and SVM. The main difference between StandardScaler and RobustScaler is that RobustScaler is less sensitive to outliers.
Parameters
The with_centering and with_scaling parameters specify if the fields should be standardized with respect to their median and interquartile range.
Syntax
fit RobustScaler <fields> [into <model name>] [with_centering=<true|false>] [with_scaling=<true|false>]
You can save RobustScaler models using the into keyword and apply new data later using the apply command.
... | apply scaling_model
You can inspect the statistics extracted by RobustScaler with the summary command.
... | summary scaling_model
Syntax constraints
RobustScaler does not support incremental fit.
Example
The following example uses RobustScaler on a test set.
... | fit RobustScaler * | ...
StandardScaler
The StandardScaler algorithm uses the scikit-learn StandardScaler algorithm to standardize data fields by scaling their mean and standard deviation to 0 and 1, respectively. This preprocessing step helps to avoid dominance of one or more fields over others in subsequent machine learning algorithms. This step is practically required for some algorithms, such as KernelPCA and SVM. This algorithm supports incremental fit.
Parameters
- The
with_meanandwith_stdparameters specify if the fields should be standardized with respect to their mean and standard deviation. - The
partial_fitparameter controls whether an existing model should be incrementally updated or not. This allows you to update an existing model using only new data without having to retrain it on the full training data set. The default is False.
Syntax
fit StandardScaler <fields> [into <model name>] [with_mean=<true|false>] [with_std=<true|false>] [partial_fit=<true|false>]
You can save StandardScaler models using the into keyword and apply new data later using the apply command.
... | apply scaling_model
You can inspect the statistics extracted by StandardScaler with the summary command.
...| summary scaling_model
Syntax constraints
- Using
partial_fit=trueon an existing model ignores the newly supplied parameters. The parameters supplied at model creation are used instead. Ifpartial_fit=falseorpartial_fitis not specified (default is false), the model specified is created and replaces the pre-trained model if one exists. - If
My_Incremental_Modeldoes not exist, the command saves the model data under the model nameMy_Incremental_Model. - If
My_Incremental_Modelexists and was trained using StandardScaler, the command updates the existing model with the new input. - If
My_Incremental_Modelexists but was not trained by StandardScaler, an error message is thrown.
Examples
The following example uses StandardScaler on a test set.
... | fit StandardScaler * | ...
The following example includes the partial_fit parameter.
| inputlookup track_day.csv | fit StandardScaler "batteryVoltage", "engineCoolantTemperature", "engineSpeed" partial_fit=true into My_Incremental_Model
Regressors
Regressor algorithms predict the value of a numeric field.
AutoPrediction
AutoPrediction automatically determines the data type as categorical or numeric. AutoPrediction then invokes the RandomForestRegressor algorithm to carry out the prediction. For further details, see RandomForestRegressor. AutoPrediction also executes the data split for training and testing during the fit process, eliminating the need for a separate command or macro. AutoPrediction uses particular cases to determine the data type, and uses the train_test_split function from sklearn to perform the data split. The kfold cross-validation command can be used with AutoPrediction. See, K-fold_cross-validation.
Parameters
- Use the
target_typeparameter to specify the target field as numeric or categorical. - The
target_typeparameter default is auto. When auto is used, AutoPrediction automatically determines the target field type. - AutoPrediction uses the following data types to determine the
target_typefield as categorical:- Data of type
bool,str, ornumpy.object - Data of type
intand thecriterionoption is specified
- Data of type
- AutoPrediction determines the
target_typefield as numeric for all other cases. - The
test_split_ratiospecifies the splitting of data for model training and model validation. Value must be a float between 0 (inclusive) and 1 (exclusive). - The
test_split_ratiodefault is 0. A value of 0 means all data points get used to train the model.- A
test_split_ratiovalue of 0.3, for example, means 30% for the data points get used for testing and 70% are used for training.
- A
- Use
n_estimatorsto optionally specify the number of trees. - Use
max_depthto optionally set the maximum depth of the tree. - Specify the
criterionvalue for classification (categorical) scenarios. - Ignore the
criterionvalue for regression (numeric) scenarios.
Syntax
fit AutoPrediction Target from Predictors* into PredictorModel target_type=<auto|numeric|categorical> test_split_ratio=<[0-1]>[n_estimators=<int>] [max_depth=<int>] [criterion=<gini | entropy>] [random_state=<int>][max_features=<str>] [min_samples_split=<int>] [max_leaf_nodes=<int>]
You can save AutoPrediction models using the into keyword and apply the saved model later to new data using the apply command.
... | apply PredictorModel
You can inspect the model learned by AutoPrediction with the summary command.
.... | summary PredictorModel
Syntax constraints
- AutoPrediction does not support
partial_fit. - Regression performance output columns for RMSE and rSquared only appear if the
target_typeis numeric. - Classification performance output columns for accuracy, f1, precision, and recall only appear if the
target_typeis categorical.
Example
The following example uses AutoPrediction on a test set.
| fit AutoPrediction random_state=42 sepal_length from * into auto_regress_model test_split_ratio=0.3 random_state=42
DecisionTreeRegressor
The DecisionTreeRegressor algorithm uses the scikit-learn DecisionTreeRegressor estimator to fit a model to predict the value of numeric fields. The kfold cross-validation command can be used with DecisionTreeRegressor. See, K-fold_cross-validation.
For descriptions of the max_depth, random_state, max_features, min_samples_split, max_leaf_nodes, and splitter parameters, see the scikit-learn documentation at http://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeRegressor.html.
Parameters
To specify the maximum depth of the tree to summarize, use the limit argument. The default value for the limit argument is 5.
| summary model_DTC limit=10
Syntax
fit DecisionTreeRegressor <field_to_predict> from <explanatory_fields> [into <model_name>] [max_depth=<int>] [max_features=<str>] [min_samples_split=<int>] [random_state=<int>] [max_leaf_nodes=<int>] [splitter=<best|random>]
You can save DecisionTreeRegressor models using the into keyword and apply it to new data later using the apply command.
... | apply model_DTR
You can inspect the decision tree learned by DecisionTreeRegressor with the summary command.
... | summary model_DTR
You can get a JSON representation of the tree by giving json=t as an argument to the summary command.
... | summary model_DTR json=t
Example
The following example uses DecisionTreeRegressor on a test set.
... | fit DecisionTreeRegressor temperature from date_month date_hour into temperature_model | ...
ElasticNet
The ElasticNet algorithm uses the scikit-learn ElasticNet estimator to fit a model to predict the value of numeric fields. ElasticNet is a linear regression model that includes both L1 and L2 regularization and is a generalization of Lasso and Ridge. The kfold cross-validation command can be used with ElasticNet. See, K-fold_cross-validation.
For descriptions of the fit_intercept, normalize, alpha, and l1_ratio parameters, see the scikit-learn documentation at http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.ElasticNet.html.
Syntax
fit ElasticNet <field_to_predict> from <explanatory_fields> [into <model name>] [fit_intercept=<true|false>] [normalize=<true|false>] [alpha=<int>] [l1_ratio=<int>]
You can save ElasticNet models using the into keyword and apply new data later using the apply command.
... | apply temperature_model
You can inspect the coefficients learned by ElasticNet with the summary command.
... | summary temperature_model
Example
The following example uses ElasticNet on a test set.
... | fit ElasticNet temperature from date_month date_hour normalize=true alpha=0.5 | ...
GradientBoostingRegressor
This algorithm uses the GradientBoostingRegressor algorithm from scikit-learn to build a regression model by fitting regression trees on the negative gradient of a loss function. The kfold cross-validation command can be used with GradientBoostingRegressor. See, K-fold_cross-validation.
For further information see the scikit-learn documentation at http://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html
Syntax
fit GradientBoostingRegressor <field_to_predict> from <explanatory_fields> [into <model_name>] [loss=<ls|lad|huber|quantile>] [max_features=<str>] [learning_rate=<float>] [min_weight_fraction_leaf=<float>] [alpha=<float>] [subsample=<float>] [n_estimators=<int>] [max_depth=<int>] [min_samples_split=<int>] [min_samples_leaf=<int>] [max_leaf_nodes=<int>] [random_state=<int>]
You can use the apply method to apply the trained model to the new data.
...|apply temperature_model
You can inspect the features learned by GradientBoostingRegressor with the summary command.
... | summary temperature_model
Example
The following example uses the GradientBoostingRegressor algorithm to fit a model and saves that model as temperature_model.
... | fit GradientBoostingRegressor temperature from date_month date_hour into temperature_model | ...
KernelRidge
The KernelRidge algorithm uses the scikit-learn KernelRidge algorithm to fit a model to predict numeric fields. This algorithm uses the radial basis function (rbf) kernel by default. The kfold cross-validation command can be used with KernelRidge. See, K-fold_cross-validation.
For details, see the scikit-learn documentation at http://scikit-learn.org/stable/modules/generated/sklearn.kernel_ridge.KernelRidge.html.
Parameters
The gamma parameter controls the width of the rbf kernel. The default value is 1/ number of fields.
Syntax
fit KernelRidge <field_to_predict> from <explanatory_fields> [into <model_name>] [gamma=<float>]
You can save KernelRidge models using the into keyword and apply new data later using the apply command.
... | apply sla_model
Syntax constraints
You cannot inspect the model learned by KernelRidge with the summary command.
Example
The following example uses KernelRidge on a test set.
... | fit KernelRidge temperature from date_month date_hour into temperature_model
Lasso
The Lasso algorithm uses the scikit-learn Lasso estimator to fit a model to predict the value of numeric fields. Lasso is like LinearRegression, but it uses L1 regularization to learn a linear models with fewer coefficients and smaller coefficients. Lasso models are consequently more robust to noise and resilient against overfitting. The kfold cross-validation command can be used with Lasso. See, K-fold_cross-validation.
For descriptions of the alpha, fit_intercept, and normalize parameters, see the scikit-learn documentation at http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Lasso.html.
Parameters
- The
alphaparameter controls the degree of L1 regularization. - The
fit_interceptparameter specifies whether the model should include an implicit intercept term. The default value is True.
Syntax
fit Lasso <field_to_predict> from <explanatory_fields> [into <model name>] [alpha=<float>] [fit_intercept=<true|false>] [normalize=<true|false>]
You can save Lasso models using the into keyword and apply new data later using the apply command.
... | apply temperature_model
You can inspect the coefficients learned by Lasso with the summary command.
... | summary temperature_model
Example
The following example uses Lasso on a test set.
... | fit Lasso temperature from date_month date_hour | ...
LinearRegression
The LinearRegression algorithm uses the scikit-learn LinearRegression estimator to fit a model to predict the value of numeric fields. The kfold cross-validation command can be used with LinearRegression. See, K-fold_cross-validation.
Parameters
The fit_intercept parameter specifies whether the model should include an implicit intercept term. The default value is True.
Syntax
fit LinearRegression <field_to_predict> from <explanatory_fields> [into <model name> [fit_intercept=<true|false>] [normalize=<true|false>]
You can save LinearRegression models using the into keyword and apply new data later using the apply command.
... | apply temperature_model
You can inspect the coefficients learned by LinearRegression with the summary command.
... | summary temperature_model
Example
The following example uses LinearRegression on a test set.
... | fit LinearRegression temperature from date_month date_hour into temperature_model | ..
RandomForestRegressor
The RandomForestRegressor algorithm uses the scikit-learn RandomForestRegressor estimator to fit a model to predict the value of numeric fields. The kfold cross-validation command can be used with RandomForestRegressor. See, K-fold_cross-validation.
For descriptions of the n_estimators, random_state, max_depth, max_features, min_samples_split, and max_leaf_nodes parameters, see the scikit-learn documentation at http://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestRegressor.html.
Syntax
fit RandomForestRegressor <field_to_predict> from <explanatory_fields> [into <model name>] [n_estimators=<int>] [max_depth=<int>] [random_state=<int>] [max_features=<str>] [min_samples_split=<int>] [max_leaf_nodes=<int>]
You can save RandomForestRegressor models using the into keyword and apply new data later using the apply command.
... | apply temperature_model
You can list the features that were used to fit the model, as well as their relative importance or influence with the summary command.
... | summary temperature_model
Example
The following example uses RandomForestRegressor on a test set.
... | fit RandomForestRegressor temperature from date_month date_hour into temperature_model | ...
Ridge
The Ridge algorithm uses the scikit-learn Ridge estimator to fit a model to predict the value of numeric fields. Ridge is like LinearRegression, but it uses L2 regularization to learn a linear models with smaller coefficients, making the algorithm more robust to collinearity. The kfold cross-validation command can be used with Ridge. See, K-fold_cross-validation.
For descriptions of the fit_intercept, normalize, and alpha parameters, see the scikit-learn documentation at http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Ridge.html.
Parameters
The alpha parameter specifies the degree of regularization. The default value is 1.0.
Syntax
fit Ridge <field_to_predict> from <explanatory_fields> [into <model name>] [fit_intercept=<true|false>] [normalize=<true|false>] [alpha=<int>]
You can save Ridge models using the into keyword and apply new data later using the apply command.
... | apply temperature_model
You can inspect the coefficients learned by Ridge with the summary command.
... | summary temperature_model
Example
The following example uses Ridge on a test set.
... | fit Ridge temperature from date_month date_hour normalize=true alpha=0.5 | ...
SGDRegressor
The SGDRegressor algorithm uses the scikit-learn SGDRegressor estimator to fit a model to predict the value of numeric fields. The kfold cross-validation command can be used with SGDRegressor. See, K-fold_cross-validation. This algorithm supports incremental fit.
Parameters
- The
partial_fitparameter controls whether an existing model should be incrementally updated or not. This allows you to update an existing model using only new data without having to retrain it on the full training data set. The default is False. - The
fit_intercept=<true|false>parameter determines whether the intercept should be estimated or not. - The
fit_intercept=<true|false>parameter default is True. - The
n_iter=<int>parameter is the number of passes over the training data also known as epochs. The default is 5.- The number of iterations is set to 1 if using
partial_fit.
- The number of iterations is set to 1 if using
- The
penalty=<l2|l1|elasticnet>parameter set the penalty or regularization term to be used. The default is l2. - The
learning_rate=<constant|optimal|invscaling>parameter is the learning rate.- constant: eta = eta0
- optimal: eta = 1.0/(alpha * t)
- invscaling: eta = eta0 / pow(t, power_t)
- default is
invscaling.
- The
l1_ratio=<float>parameter is the Elastic Net mixing parameter, with 0 <= l1_ratio <= 1. Default is 0.15.- l1_ratio=0 corresponds to L2 penalty
- l1_ratio=1 to L1
- The
alpha=<float>parameter is the constant that multiplies the regularization term. Default is 0.0001.- Also used to compute
learning_ratewhen set to Optimal.
- Also used to compute
- The
eta0=<float>parameter is the initial learning rate. Default is 0.01. - The
power_t=<float>parameter is the exponent for inverse scaling learning rate. Default is 0.25. - The
random_state=<int>parameter is the seed of the pseudo random number generator to use when shuffling the data.
Syntax
fit SGDRegressor <field_to_predict> from <explanatory_fields> [into <model name>] [partial_fit=<true|false>] [fit_intercept=<true|false>] [random_state=<int>] [n_iter=<int>] [l1_ratio=<float>] [alpha=<float>] [eta0=<float>] [power_t=<float>] [penalty=<l1|l2|elasticnet>] [learning_rate=<constant|optimal|invscaling>]
You can save SGDRegressor models using the into keyword and apply new data later using the apply command.
... | apply temperature_model
You can inspect the coefficients learned by SGDRegressor with the summary command.
... | summary temperature_model
Syntax constraints
- If
My_Incremental_Modeldoes not exist, the command saves the model data under the model nameMy_Incremental_Model. - If
My_Incremental_Modelexists and was trained using SGDRegressor, the command updates the existing model with the new input. - If
My_Incremental_Modelexists but was not trained by SGDRegressor, an error message displays. - Using
partial_fit=trueon an existing model ignores the newly supplied parameters. The parameters supplied at model creation are used instead. - If
partial_fit=falseorpartial_fitis not specified the model specified is created and replaces the pre-trained model if one exists.
Examples
The following example uses SGDRegressor on a test set.
... | fit SGDRegressor temperature from date_month date_hour into temperature_model | ...
The following example includes thepartial_fit parameter.
| inputlookup server_power.csv | fit SGDRegressor "ac_power" from "total-cpu-utilization" "total-disk-accesses" partial_fit=true into My_Incremental_Model
System Identification
Use the System Identification algorithm to model both non-linear and linear relationships. In a typical use case you predict a number of target fields from their past values as well as from the past and current values of other feature fields. The System Identification algorithm is powered by a multi-layered, fully-connected neural network. System Identification supports incremental fit.
The System Identification algorithm only works with numeric field values.
Parameters
- The wildcard character is supported within target and feature fields.
- Use the
dynamicsparameter to specify the amount of lag to be used for each variable.- The
dynamicsparameter is required. - Must be a list of non-negative integers separated by hyphens.
- The number of non-negative integers listed must equal the number of target variables plus the number of feature variables.
- The non-negative integers align with target and feature variables based on the order in which they are written.
- One dynamic value is matched with each wildcard and the same amount applies to all fields matched by that wildcard.
- The
- The
conf_intervalparameter specifies the confidence interval percentage for the prediction.- Value must be between 1 and 99.
- A larger number means a greater tolerance for prediction uncertainty.
- Default value is 95.
- The
conf_intervalnumber used with thefitcommand does not need to be the same number used with theapplycommand.
- The
layersoption specifies the number of hidden layers and their sizes in the neural network.- Must be a list of positive integers separated by hyphens.
- Option defaults to
64-64for two layers, each of a size of 64.
- Use the
epochsoption to specify the number of iterations during training.- Must be a positive integer.
- Default value for
epochsis 500.
Syntax
| fit SystemIdentification <target-fields> from <feature-fields> dynamics=<int-int-...> [conf_interval=<int>] [layers=<int-int-...>] [epochs=<int>] [into <model-name>]
You can apply the saved model to new data with the apply command.
| apply <model-name> [conf_interval=<int>]
You can inspect the model learned by System Identification with the summary command.
| summary <model-name>
Syntax constraints
System identification cannot be used with K-fold cross validation.
Examples
The following example uses three lags of Expenses, two lags of HR1, two lags of HR2, and three lags of ERP.
| inputlookup app_usage.csv | fit SystemIdentification Expenses from HR1 HR2 ERP dynamics=3-2-2-3
The following example uses three lags of Expenses, two lags of all fields that starts with HR, and three lags of ERP.
| inputlookup app_usage.csv | fit SystemIdentification Expenses from HR* ERP dynamics=3-2-3
The following example uses a fully-connected neural network with three hidden layers, each with a layer size of 64. The total number of layers in the neural network is five and comprised of one input layer, three hidden layers, and one output layer.
| inputlookup app_usage.csv | fit SystemIdentification Expenses from HR1 HR2 ERP dynamics=3-1-2-3 layers=64-64-64
The following example uses System Identification on a test set.
Time Series Analysis
Forecasting algorithms, also known as time series analysis, provide methods for analyzing time series data in order to extract meaningful statistics and other characteristics of the data, and forecast its future values.
ARIMA
The Autoregressive Integrated Moving Average (ARIMA) algorithm uses the StatsModels ARIMA algorithm to fit a model on a time series for better understanding and/or forecasting its future values. An ARIMA model can consist of autoregressive terms, moving average terms, and differencing operations. The autoregressive terms express the dependency of the current value of time series to its previous ones.
The moving average terms, also called random shocks or white noise, model the effect of previous forecast errors on the current value. If the time series is non-stationary, differencing operations are used to make it stationary. A stationary process is a stochastic process in that its probability distribution does not change over time.
See the StatsModels documentation at http://statsmodels.sourceforge.net/devel/generated/statsmodels.tsa.arima_model.ARIMA.html for more information.
It is highly recommended to send the time series through timechart before sending it into ARIMA to avoid non-uniform sampling time. If _time is not to be specified, using timechart is not necessary.
Parameters
- The time series should not have any gaps or missing data otherwise ARIMA will complain. If there are missing samples in the data, using a bigger span in timechart or using streamstats to fill in the gaps with average values can do the trick.
- When chaining ARIMA output to another algorithm (i.e. ARIMA itself), keep in mind the length of the data is the length of the original data +
forecast_k. If you want to maintain theholdbackposition, you need to add the number inforecast_kto yourholdbackvalue. - ARIMA requires the
orderparameter to be specified at fitting time. Theorderparameter needs three values:- Number of autoregressive (AR) parameters
- Number of differencing operations (D)
- Number of moving average (MA) Parameters
- The
forecast_k=<int>parameter tells ARIMA how many points into the future should be forecasted. If_timeis specified during fitting along with thefield_to_forecast, ARIMA will also generate the timestamps for forecasted values. By default,forecast_kis zero. - The
conf_interval=<1..99>parameter is the confidence interval in percentage around forecasted values. By default it is set to 95%. - The
holdback=<int>parameter is the number of data points held back from the ARIMA model. This is useful for comparing the forecast against known data points. By default, holdback is zero.
Syntax
fit ARIMA [_time] <field_to_forecast> order=<int>-<int>-<int> [forecast_k=<int>] [conf_interval=<int>] [holdback=<int>]
Syntax constraints
- ARIMA supports one time series at a time.
- ARIMA models cannot be saved and used at a later time in the current version.
- Scoring metric values are based on all data and not on the
holdbackperiod data.
Example
The following example uses ARIMA on a test set.
... | fit ARIMA Voltage order=4-0-1 holdback=10 forecast_k=10
StateSpaceForecast
StateSpaceForecast is a forecasting algorithm for time series data in MLTK. It is based on Kalman filters. The algorithm supports incremental fit.
Advantages of StateSpaceForecast over ARIMA include:
- Persists models created using the
fitcommand that can then be used withapply. - A
specialdaysfield allows you to account for the effects of a specified list of special days. - It is automatic in that you do no need to choose parameters or mode.
- Supports multivariate forecasting.
Parameters
- By default the historical data results from running the
fitcommand are not shown. To modify this behavior setoutput_fit=True. - The
fieldssegment of the search supports the wildcard (*) character. - Use the
targetfield to specify fields from which to forecast using historical data and other values. - The
targetfield is a comma-separated list of fields that can be univariate or multivariate. These fields must be specified during thefitprocess.- Optionally use the
targetfield to fit multiple fields during thefitprocess but apply only a selection of those target fields during theapplyprocess.
- Optionally use the
- If the
targetfield is not specified, then all fields will be forecast together using historical data. - The
specialdaysfield specifies the field that indicates effects due to special days such as holidays. - The
specialdaysfield values must be numeric and are typically 0 and 1, with 1 indicating the existence of a special day effect. Null values are treated as 0. - The majority of use cases have no
specialdays. Events that occur regularly and frequently such as weekends should not be treated asspecialdays. Usespecialdaysto capture events such as holiday sales. - Use
specialdaysin theapplystep if it has been specified duringfit. The same field(s) must be assigned. - Use the
periodparameter to specify if your data has a known periodicity. - If the
periodparameter is not specified it is computed automatically. - Set
period=1to treat the time series as non-periodic. - As with other MLTK algorithms, the
partial_fitparameter controls whether a model should be incrementally updated or not. This allows you to update a model using only new data without having to retrain the model on the full dataset. - The default for
partial_fitis False. - Use
update_lastto modify the behavior ofpartial_fit - The default for
update_lastis False. - If
partial_fit=TrueStateSpaceForecast first updates the model parameters and then predicts. - If
partial_fit=Trueandupdate_last=TrueStateSpaceForecast first predicts and then updates the model parameters. This allows you to review the forecast before running new data through. - The
conf_interval=<1..99>parameter is the confidence interval in percentage around forecasted values. Input an integer between 1 and 99 where a larger number means a greater tolerance for forecast uncertainty. The default integer is 95. - Use the
asfield to assign aliases to forecasted fields. - In univariate cases the
asfieldfield-listis a single field name. - In multivariate cases, the
asfield adheres to the following conventions:- The list must be in double quotes, separated by either spaces or commas.
- The aliases correspond to the original fields in the given order.
- The number of aliases can be smaller than the number of original fields.
- The
summarycommand lists the names of the fields used in thefitcommand step, the name of thespecialdaysfield, and the period. - The
holdbackparameter is the number of data points held back from training. This is useful for comparing the forecast against known data points. Default holdback value is 0. - If you want to maintain the
holdbackposition, add the position number inforecast_kto yourholdbackvalue. - The
forecast_kparameter tells StateSpaceForecast how many points into the future should be forecasted. If_timeis specified during fitting along with thefield_to_forecast, StateSpaceForecast also generates the timestamps for forecasted values. Default,forecast_kvalue is 0. - The
holdbackandforecast_kvalues can be of two types: an integer or a time range.- An integer specifies a number of events. An example of
forecast_k=10forecasts 10 events into the future. An example ofholdback=10withholds the last 10 events from training. - A time range takes the form
XYwhere X is a non-negative integer and Y is either empty or adheres to format in the time range table. If Y is empty, then the time range is instead interpreted as an integer or a number of events. An example ofholdback=3day forecast_k=1weekwithholds 3 days of events and forecasts 1 week's worth of events.
- An integer specifies a number of events. An example of
The actual number of events withheld and forecasted using the time range option depends on the time interval between consecutive events.
Time range Acceptable formats for Y value seconds s, sec, secs, second, seconds minutes m, min, minute, minutes hours h, hr, hrs, hour, hours days d, day, days weeks w, week, weeks months mon, month, months quarters q, qtr, qtrs, quarter, quarters years y, yr, yrs, year, years
Syntax
| fit StateSpaceForecast <fields> [from *] [specialdays=<field name>] [holdback=<int | time-range>] [forecast_k=<int | time-range>] [conf_interval=<float>] [period=<int>] [partial_fit=<true|false>] [update_last=<true|false>] [output_fit=<true|false>] [into <model name>] [as <field-list>]
You can apply the saved model to new data with the apply command.
| apply <model name> [specialdays=<field name>] [target=<fields>] [holdback=<int | time-range>] [forecast_k=<int | time-range>] [conf_interval=<float>]
You can inspect the model learned by StateSpaceForecast with the summary command.
| summary <model name>
Syntax constraints
- For univariate analysis the
fieldsparameter is a single field, but for multivariate analysis it is a list of fields. - For multivariate analysis, only one
specialdaysfield can be specified and it applies to all the fields. - The
specialdaysfield values must be numeric. - Null values in the
specialdaysfield are treated as 0. - Double quotes are required around field lists.
- Scoring metric values are based on the
holdbackperiod data.
Examples
The following is a univariate example of StateSpaceForecast on a test set. The example is considered univariate as there is only a single field following | fit StateSpaceForecast. The example dataset is derived from the milk.csv dataset that ships with MLTK. The milk2.csv has a new column named holiday. This column has two values 0 and 1. The 0 value represents no holiday and 1 value represents a holiday for the associated date. The 1 values were set randomly.
| inputlookup milk2.csv | fit StateSpaceForecast milk_production from * specialdays=holiday into milk_model | apply milk_model specialdays=holiday forecast_k=30
The following is a multivariate example of StateSpaceForecast on a test set. The syntax is the same as that in the univariate example, except that this case has a list of fields (CRM, ERP, and Expenses) following | fit StateSpaceForecast, making it multivariate.
| inputlookup app_usage.csv | fields CRM ERP Expenses | fit StateSpaceForecast CRM ERP Expenses holdback=12 into app_usage_model as "crm, erp"
The following example is also multivariate and includes the target field. In this example the fields of CRM and ERP are forecast using historical data and the Expenses field. The apply command is used against the model created in the fit command step, resulting in the app_usage_model model.
Double quotes are required around any field list.
| inputlookup app_usage.csv | fields CRM ERP Expenses | apply app_usage_model target="CRM, ERP" forecast_k=36 holdback=36
The following example is again multivariate but without the target field. This example forecasts the fields CRM, ERP, and Expenses using historical data.
| inputlookup app_usage.csv | fields CRM ERP Expenses | apply app_usage_model forecast_k=36 holdback=36
The following example uses the wildcard (*) character to specify the three fields of total_accidents, front_accidents, and rear_accidents.
| inputlookup UKfrontrearseatKSI.csv | eval total_accidents='British drivers KSI' | eval front_accidents='front seat KSI' | eval rear_accidents='rear seat KSI' | fit StateSpaceForecast *accidents holdback=30 from * forecast_k=10
The following example shows how to improve your output with StateSpaceForecast.
| inputlookup cyclical_business_process_with_external_anomalies.csv | eval holiday=if(random()%100<98,0,1) | fit StateSpaceForecast logons from logons into My_Model forecast_k=3000
Adding of the SPL line period=2016 could improve the output, but would not account for the period being seven days rather than twenty-four hours.
| inputlookup cyclical_business_process_with_external_anomalies.csv | table _time,logons | eval holiday=if(random()%100<98,0,1) | eval dayOfWeek=strftime(_time,"%a") | eval holidayWeekend=case(in(dayOfWeek,"Sat","Sun"),1,true(),0) | apply MyBadModel specialdays=holidayWeekend forecast_k=3000 | eval old_predict='predicted(logons)' | eval dayOfWeek=strftime(_time,"%a") | eval holidayWeekend=case(in(dayOfWeek,"Sat","Sun"),1,true(),0) | apply My_Model specialdays=holidayWeekend holdback=3000 forecast_k=3000
Utility Algorithms
These utility algorithms are not machine learning algorithms, but provide methods to calculate data characteristics. These algorithms facilitate the process of algorithm selection and parameter selection. See the StatsModels documentation at http://www.statsmodels.org/stable/generated/statsmodels.tsa.stattools.acf.html for more information.
ACF (autocorrelation function)
ACF (autocorrelation function) calculates the correlation between a sequence and a shifted copy of itself, as a function of shift. Shift is also referred to as lag or delay.
Parameters
- The
kparameter specifies the number of lags to return autocorrelation for. By defaultkis 40. - The
fftparameter specifies whether ACF is computed via Fast Fourier Transform (FFT). By defaultfftis False. - The
conf_intervalparameter specifies the confidence interval in percentage to return. By defaultconf_intervalis set to 95.
Syntax
fit ACF <field> [k=<int>] [fft=true|false] [conf_interval=<int>]
Example
The following example uses ACF (autocorrelation function) on a test set.
... | fit ACF logins k=50 fft=true conf_interval=90
PACF (partial autocorrelation function)
PACF (partial autocorrelation function) gives the partial correlation between a sequence and its lagged values, controlling for the values of lags that are shorter than its own. See the StatsModels documentation at http://www.statsmodels.org/stable/generated/statsmodels.tsa.stattools.pacf.html for more information.
Parameters
- The
kparameter specifies the number of lags to return partial autocorrelation for. By defaultkis 40. - The
methodparameter specifies which method for the calculation to use. By defaultmethodis unbiased. - The
conf_intervalparameter specifies the confidence interval in percentage to return. By defaultconf_intervalis set to 95.
Syntax
fit PACF <field> [k=<int>] [method=<ywunbiased|ywmle|ols>] [conf_interval=<int>]
Example
The following example uses PACF (partial autocorrelation function) on a test set.
... | fit PACF logins k=20 conf_interval=90
| Custom visualizations in the Splunk Machine Learning Toolkit | Import a machine learning algorithm from Splunkbase |
This documentation applies to the following versions of Splunk® Machine Learning Toolkit: 5.5.0
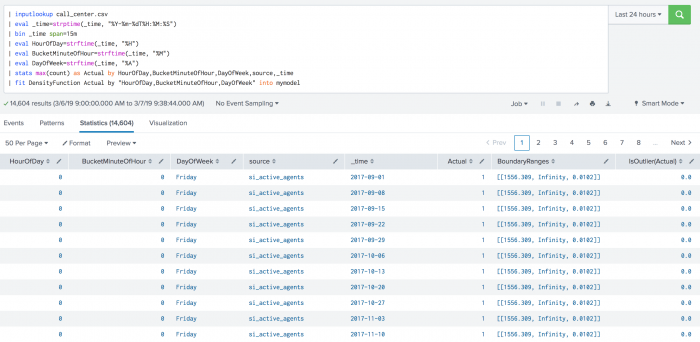
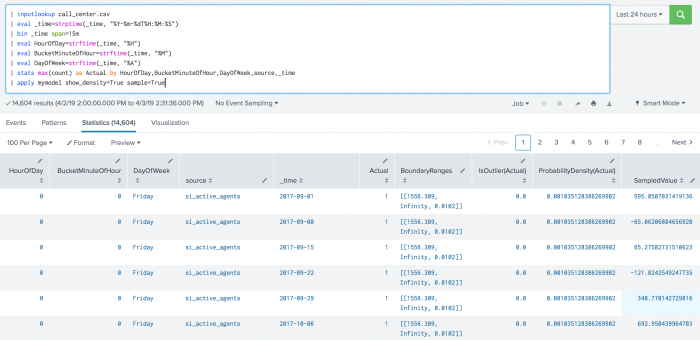
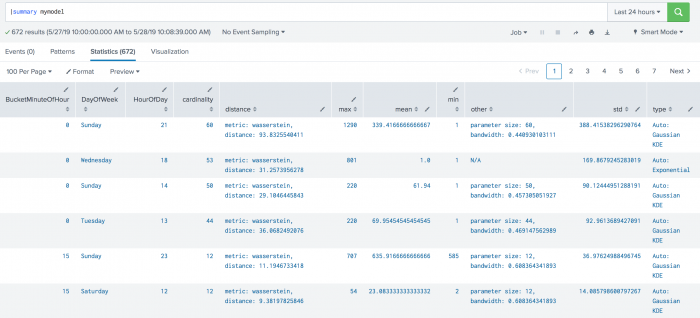
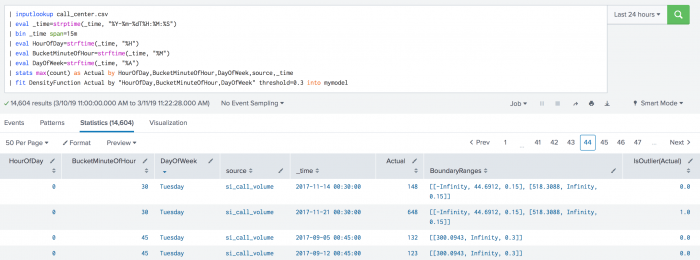
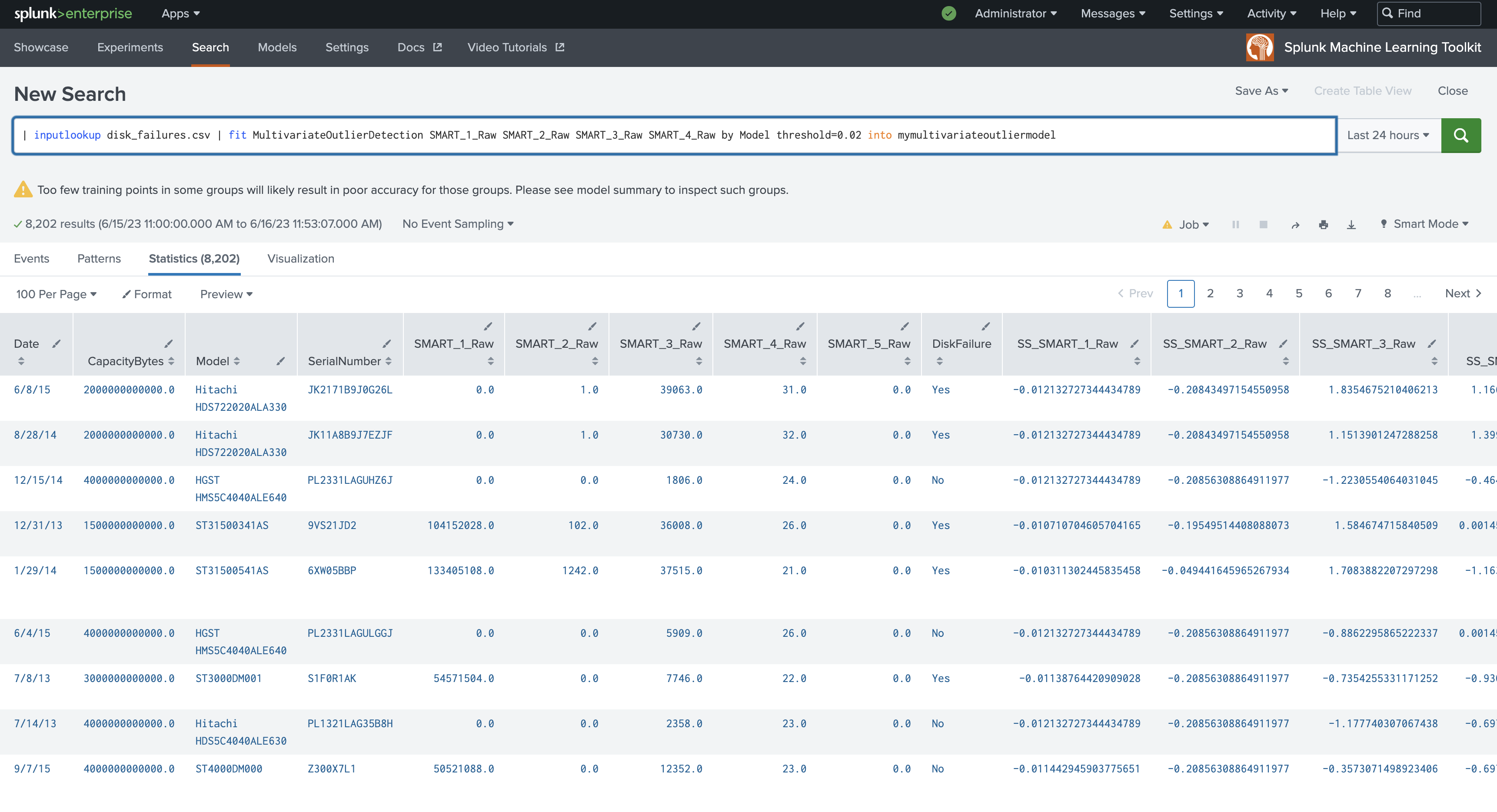
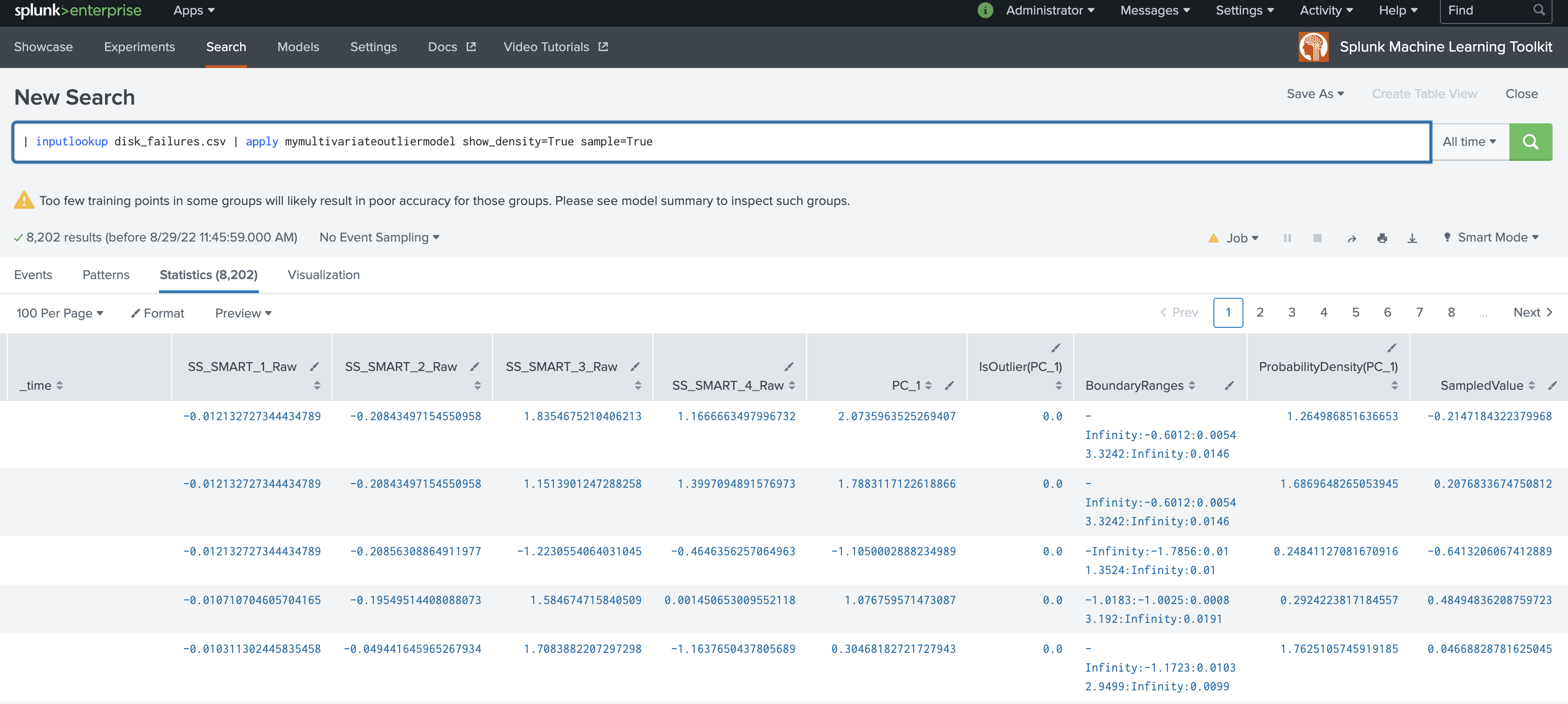
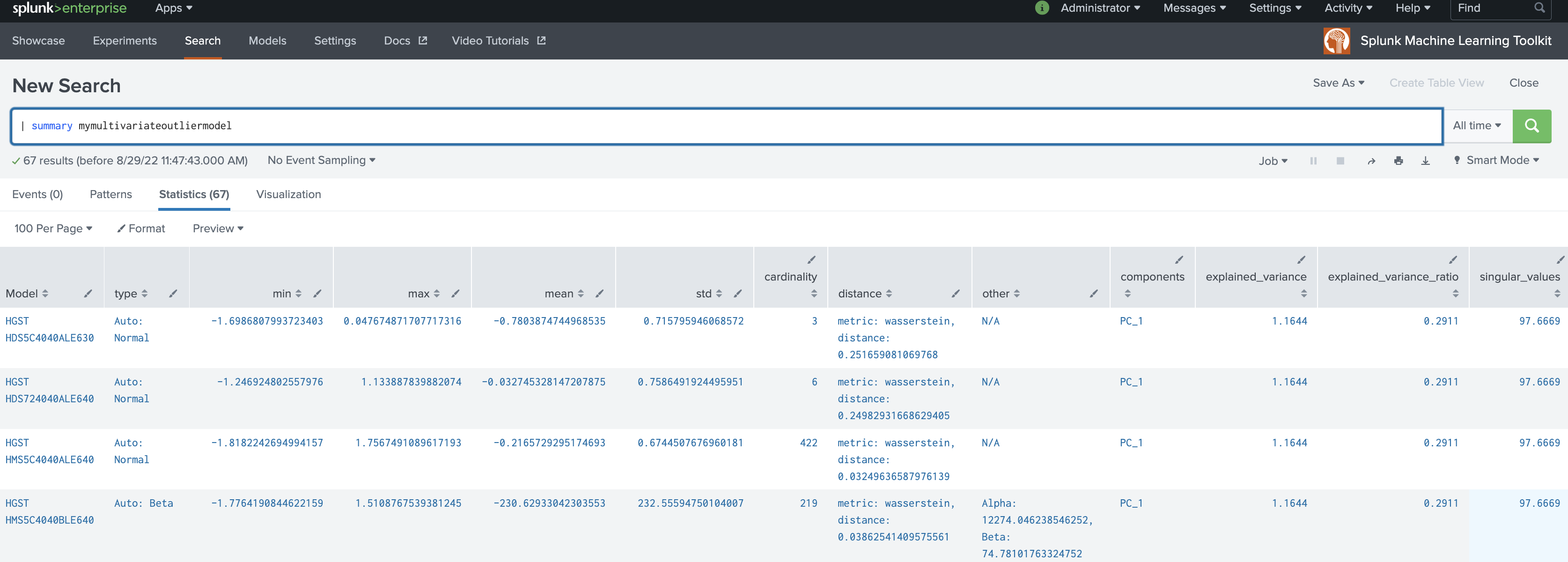



 Download manual
Download manual
Feedback submitted, thanks!