Forecast Time Series Classic Assistant workflow
Classic Assistants enable machine learning through a guided user interface. The Forecast Time Series Classic Assistant predicts the next value in a sequence of time series data. The result includes both the predicted value and a measure of the uncertainty of that prediction. Forecasting makes predictions based on time series data from the past.
The following visualization shows a time series and the split between the training and testing data.
Algorithms
The Forecast Time Series assistant can use the following algorithms to make predictions:
- State-space method using Kalman filter
- AutoRegressive Integrated Moving Average (ARIMA)
Forecast Time Series
Input the data and select the field you want to forecast.
Workflow
Follow these steps for the Forecast Time Series Classic Assistant.
- From the MLTK navigation bar select Classic > Assistants > Forecast Time Series.
- Run a search, and be sure to select a date range.
- Select an algorithm from the
Algorithmdrop-down menu.
If you are not sure which algorithm to choose, start with the default Kalman filter algorithm. - Select the field from which you want to base the forecast from the
Field to Forecast.
The Field to Forecast list is populated with fields from the search. - Select the parameters. Refer to the following table as a guide.
If Then You chose the Kalman filter algorithm. Select a forecasting method. These methods consider subsets of features such as local level (an average of recent values), trend (a slope of line that fits through recent values), and seasonality (repeating patterns). You chose the ARIMA algorithm Specify the values for AR (autoregressive) - p, I (integrated) - d, MA (moving average) - q parameters.
For example, AR(1) means you would forecast future values by looking at 1 past value. I(1) means it took 1 difference, where each data point was subtracted from the one that follows it, to make the time series stationary. MA(1) means you would forecast future values using 1 previous prediction error.
- Specify the
Future Timespan, which indicates how far beyond the data you want to forecast.
The size of the confidence interval is used to gauge how confident the algorithm is in its forecast. - Specify the number of values to withhold in the
Holdbackfield, . Decide how many search results to use for validating the quality of the forecast.
The larger the withholding, the fewer values available to train your model. - Specify the percentage of the future data you expect to fall inside of the confidence envelope with the
Confidence Intervalfield.
If Then You chose the Kalman filter algorithm. Select the Period, which indicates the period of any known repeating patterns in the data to assist the algorithm.
For example, if your data includes monthly sales data that follows annual patterns, specify 12 for the period.
- Click Forecast.
Interpret and validate
After you forecast a time series, review your results in the following tables and visualizations.
| Result | Definition |
|---|---|
| Raw Data Preview | This displays the raw data from the search. |
| Forecast | This graphs displays the actual value as a solid line and the predicted value as a dotted line, surrounded by a confidence envelope.
Values that fall outside the confidence envelope are outliers. A vertical line indicates where training data stops and test data begins. When the real data ends, forecasted values are displayed in shades of green. The larger the envelope, the less confidence we have about forecasts around that time. The size of the envelope is directly related to the specified confidence interval percentage. |
| R2 Statistic | This statistic explains how well the model explains the variability of the result. 100% (a value of 1) means the model fits perfectly. The closer the value is to 1 (100%), the better the result. |
| Root Mean Squared Error | This statistic explains the variability of the result, essentially the standard deviation of the residual. The formula takes the difference between actual and predicted values, squares this value, takes an average, and then takes a square root. The result is an absolute measure of fit, the smaller the number the better the fit. These values only apply to one dataset and are not comparable to values outside of it. |
| Prediction Outliers | This result shows the total number of outliers detected. |
Predicting with the ARIMA algorithm
When predicting using the ARIMA algorithm, additional autocorrelation panels are present. Autocorrelation charts can be used to estimate and identify the three main parameters for the model:
- the autoregressive component
p - the integrated component or order of differencing
d - the moving average component
q
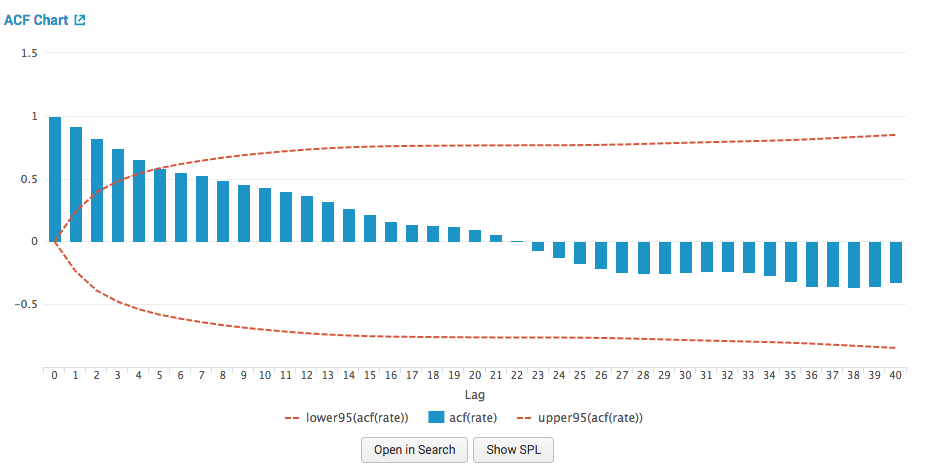
ACF: Autocorrelation function chart
The autocorrelation function chart shows the predicted field's autocorrelations at various lags, surrounded by confidence interval lines. For example, the column at lag 1 shows the amount of correlation between the time series and a lagged version of itself.
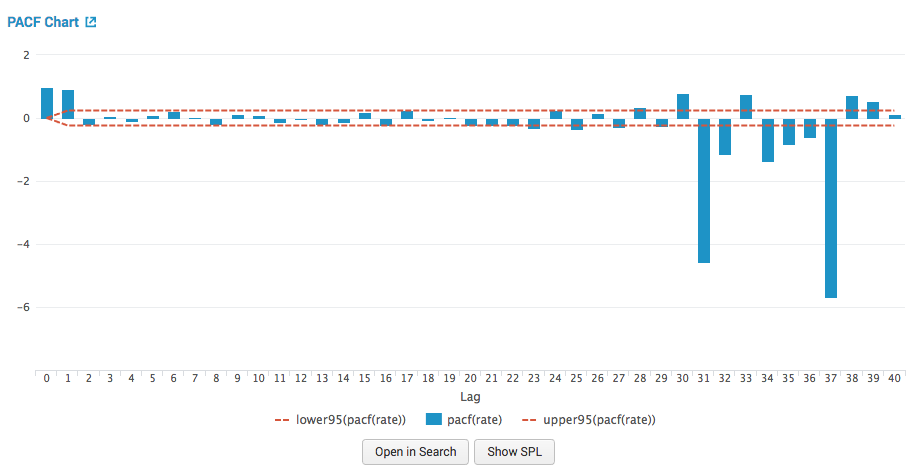
PACF: Partial autocorrelation function chart
The partial autocorrelation function chart shows the predicted field's autocorrelations at various lags while controlling for the amount of correlation contributed by earlier lag points. This chart is also surrounded by confidence interval lines. For example, the column at lag 2 shows the amount of correlation between the time series and a lagged version of itself, while removing the correlation contributed by the lag 1 data points.
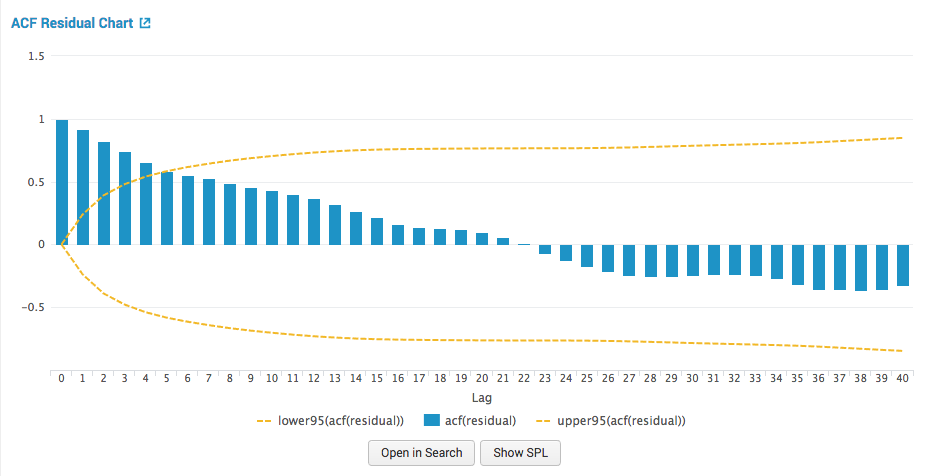
ACF Residual: Autocorrelation function residual chart
The autocorrelation function residual chart shows prediction errors. The errors are the difference between the series and the predictions. The ACF of the residuals should be close to zero. If the errors are highly correlated, the model might be poorly parameterized, or the series might not be stationary.
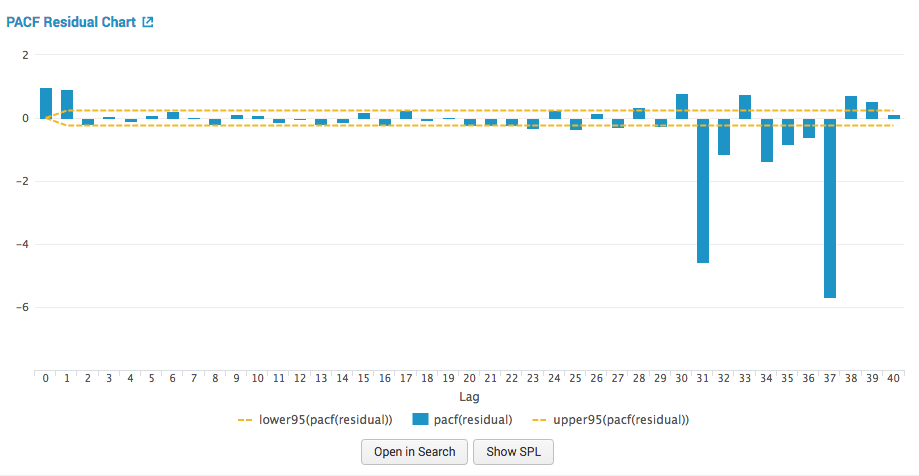
PACF Residual: partial autocorrelation function residual chart
The partial autocorrelation function chart shows prediction errors. The errors are the difference between the series and the predictions. The PACF of the residuals should be close to zero. If the errors are highly correlated, the model might be poorly parameterized or the series might not be stationary.
Refine the forecast
After you create a forecast, you can select a different algorithm to see if a different choice yields better results. The quality of the forecast primarily depends upon how predictable the data is.
Deploy the forecast
After you validate and refine the forecast, deploy the forecast.
Within the Classic Assistant framework
- At the bottom of the visualization of the forecast, click Schedule Alert to create an alert for when a prediction meets criteria you set.
This opens a new modal/ window overlay with fields to fill out.
Outside the Classic Assistant framework
- Click Open in Search to to generate a New Search tab populated with the search query used for the visualization. This new search will open in a new browser tab, away from the Classic Assistant. You can adjust the SPL directly and see results immediately. You can also save the query as a Report, Dashboard Panel or Alert.
- Click Show SPL to generate a new modal/ window overlay populated with the search query used for the visualization. You can use this same query on a different data set.
Once you navigate away from the Classic Assistant page, you cannot return to it through the Classic or Models tabs. Classic Assistants are great for generating SPL, but may not be ideal for longer-term projects.
For more information about alerts, see Getting started with alerts in the Splunk Enterprise Alerting Manual.
| Detect Categorical Outliers Classic Assistant workflow | Cluster Numeric Events Classic Assistant workflow |
This documentation applies to the following versions of Splunk® Machine Learning Toolkit: 4.4.0, 4.4.1, 4.4.2, 4.5.0, 5.0.0, 5.1.0, 5.2.0, 5.2.1, 5.2.2, 5.3.0, 5.3.1

 Download manual
Download manual
Feedback submitted, thanks!